Inductance and Charge Redistribution

[Ayesha02]

Ok, we know that $i(t)$ is growing, and since $i(t)=Q'(t)$, then $Q'(t)$ should also be growing, or, in mathematics, $Q''(t)\geq0$.
I haven't foreseen this. We definitely know that $Q'_A\leq0$ and that $Q'_B\geq0$, but I don't see how we can say anything about their second derivatives without knowing the actual functions.
Since it seems that we have no idea, I suggest we choose $Q=cQ_B(t)=c(Q_0-Q_A(t))$, where $c$ is either $1$ or $-1$, and is to be determined later.
This should work as $cQ''_B=-cQ''_A=ci'(t)$ (substitute with the expression you have found for $Q_B$ to check).

oh man!
why do I need second derivative here now:(

 

[Ayesha02]

oh man!
why do I need second derivative here now:(

could you do me a favor and send a pic of your working for this sum-- I'm going terribly wrong somewhere but i can't pinpoint it:(

 

[rude man]

So
I'm not sure I'm quite getting how to eliminate one of $Q_A$ or $Q_B$ there buddy

well, where does the care from q1 go to? Is any charge lost between the two?

="Ayesha02, post: 6336768, member: 677354"]
See
various thoughts crossing my mind-
1. I have four unknowns ( $Q_0$ ,$Q_A$ ,$Q_B$ and i ) and only 3 equations

you have 3 unknowns but can easily eliminate one of them, leaving you with 2 unknowns but related by a derivative..

 

[Ayesha02]

Instead,
Can't we consider a loop at infinity and just write the loop law simply?

 

[Ayesha02]

What an awful problem!
It's too tempting to neglect the mutual capacitance between A and B and consider only the self capacitance. However (https://en.wikipedia.org/wiki/Capacitance) points out the mutual capacitance equals the self capacitance. We end up with to capacitors "connected to infinity" and another between points A and B.

dude can u please elaborate on this?

 

[Ayesha02]

So
My textbook's solution says that :

angular frequency of the LC oscillation is w=sqrt( 2*pi*$E_0$*R*L)
And that required time is one fourth of time period

Can you explain this please @rude man @archaic

 

[archaic]

Instead of my other suggestion, you should take $Q(t)=cQ_A(t)$.
$$\frac{kQ_A(t)}{r} - \frac{k(Q_0-Q_A(t))}{r} = L\frac{di}{dt}=L\frac{d^2}{dt^2}\left(cQ_A(t)\right)\\
\implies\frac{k}{r}\left(2Q_A(t)-Q_0\right)=cL\frac{d^2Q_A(t)}{dt^2}$$
Take $f(t)=2Q_A(t)-Q_0$, this gives you $f''(t)=2Q_A''(t)$, thus
$$\frac{k}{r}f(t)=\frac{cL}{2}\frac{d^2f(t)}{dt^2}$$

 

[Ayesha02]

So
My textbook's solution says that :

angular frequency of the LC oscillation is w=sqrt( 2*pi*$E_0$*R*L)
And that required time is one fourth of time period

Can you explain this please @rude man @archaic

Can you please explain this @archaic

 

[archaic]

Can you please explain this @archaic

You have$$\frac{k}{r}f(t)=\frac{cL}{2}\frac{d^2f(t)}{dt^2}$$where $f(t)=2Q_A(t)-Q_0$. You want to find the time at which $Q_A(t)=\frac{Q_0}{2}$.
Start by solving the differential equation, and remember what I said about $c$!

 

[archaic]

You have$$\frac{k}{r}f(t)=\frac{cL}{2}\frac{d^2f(t)}{dt^2}$$where $f(t)=2Q_A(t)-Q_0$. You want to find the time at which $Q_A(t)=\frac{Q_0}{2}$.
Start by solving the differential equation, and remember what I said about $c$!

Hint: what are $Q_A(0)$ and $i(0)$?

 

[Delta2]

I am not sure I agree with all the posts here, but I believe the final equation first presented at post #37 should have a minus sign in front. coming from the fact that the voltage in an inductor is $V=-L\frac{dI}{dt}$.

Also because the "circuit" is not so local the current will vary spatially across the two ends of the inductor, so i believe we should explicitly state as a vital assumption that the current does not vary spatially but only temporally.

 

[archaic]

I am not sure I agree with all the posts here, but I believe the final equation first presented at post #37 should have a minus sign in front. coming from the fact that the voltage in an inductor is $V=-L\frac{dI}{dt}$.

Also because the "circuit" is not so local the current will vary spatially across the two ends of the inductor, so i believe we should explicitly state as a vital assumption that the current does not vary spatially but only temporally.

I have multiplied by $c$ for lack of knowledge abour the sign, and yes, it turned out to be $-1$!

 

[etotheipi]

I am not sure I agree with all the posts here, but I believe the final equation first presented at post #37 should have a minus sign in front. coming from the fact that the voltage in an inductor is $V=-L\frac{dI}{dt}$.

I think the $\frac{kQ_A(t)}{r} - \frac{k(Q_0-Q_A(t))}{r} = L\frac{di}{dt}$ is okay because that's just passive sign convention, OP just needs to be careful when substituting in $i = -\frac{dQ_A}{dt} = \frac{dQ_B}{dt}$ since you should get a negative sign out the front. From then on, it's just a mass on the end of a spring problem .

 

[archaic]

I think the $\frac{kQ_A(t)}{r} - \frac{k(Q_0-Q_A(t))}{r} = L\frac{di}{dt}$ is okay because that's just passive sign convention, OP just needs to be careful when substituting in $i = -\frac{dQ_A}{dt} = \frac{dQ_B}{dt}$ since you should get a negative sign out the front. From then on, it's just a mass on the end of a spring problem .

I have multiplied by $c$ for lack of knowledge abour the sign, and yes, it turned out to be $-1$!

Oh, a sign convention? So we don't care at all about the actual sign by analyzing the charge functions?

 

[etotheipi]

You can work it all out logically, but it's often quicker to do anything circuit related with the so-called passive sign convention

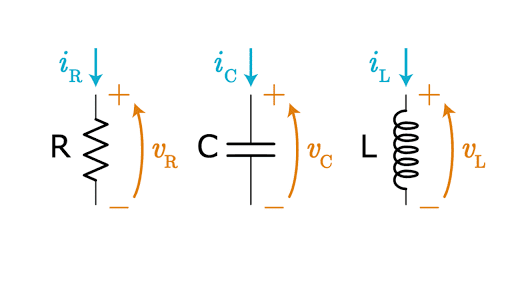
Essentially, if the reference direction for the voltage is in the opposite direction to the reference direction for current, then the formulae for passive components hold without negative signs, i.e. $v=ir$, $i = c\frac{dv}{dt}$, $v = l\frac{di}{dt}$. A consequence is that passive components have positive power. If you define the reference directions the other way around (the so-called active sign convention, which I hear isn't usually done in electrical engineering), then all of those defining equations have negative signs in them.

It just means that here we can define the reference voltage direction as from B to A (i.e. V(A) - V(B)) and the reference current direction from A to B, and not worry about getting the signs wrong.

 

[Delta2]

I think the $\frac{kQ_A(t)}{r} - \frac{k(Q_0-Q_A(t))}{r} = L\frac{di}{dt}$ is okay because that's just passive sign convention, OP just needs to be careful when substituting in $i = -\frac{dQ_A}{dt} = \frac{dQ_B}{dt}$ since you should get a negative sign out the front. From then on, it's just a mass on the end of a spring problem .

Thanks for explaining the sign convention used in circuits at post #45 but one more thing I want to ask, why do you take current to be $I=-\frac{dQ_A}{dt}=\frac{dQ_B}{dt}$ and not $I=\frac{dQ_A}{dt}=-\frac{dQ_B}{dt}$

 

[etotheipi]

Thanks for explaining the sign convention used in circuits at post #45 but one more thing I want to ask, why do you take current to be $I=-\frac{dQ_A}{dt}=\frac{dQ_B}{dt}$ and not $I=\frac{dQ_A}{dt}=-\frac{dQ_B}{dt}$

I defined the reference direction of $i$ to be in the direction from A to B, so positive current results in B gaining charge and A losing charge.

Sorry for not making that clear; I have the feeling that we defined everything in exactly the exact opposite way!

 

[Ayesha02]

I think the $\frac{kQ_A(t)}{r} - \frac{k(Q_0-Q_A(t))}{r} = L\frac{di}{dt}$ is okay because that's just passive sign convention, OP just needs to be careful when substituting in $i = -\frac{dQ_A}{dt} = \frac{dQ_B}{dt}$ since you should get a negative sign out the front. From then on, it's just a mass on the end of a spring problem .

@etotheipi
Can you explain how do i solve the equation after substituting ,$i$ ?

 

[etotheipi]

@Ayesha02 Try what @archaic suggested (I have substituted for $c$ for clarity):

Instead of my other suggestion, you should take $Q(t)=-Q_A(t)$.
$$\frac{kQ_A(t)}{r} - \frac{k(Q_0-Q_A(t))}{r} = L\frac{di}{dt}=L\frac{d^2}{dt^2}\left(-Q_A(t)\right)\\
\implies\frac{k}{r}\left(2Q_A(t)-Q_0\right)=-L\frac{d^2Q_A(t)}{dt^2}$$
Take $f(t)=2Q_A(t)-Q_0$, this gives you $f''(t)=2Q_A''(t)$, thus
$$\frac{k}{r}f(t)=\frac{-L}{2}\frac{d^2f(t)}{dt^2}$$

That last equation is the same as $\frac{-2k}{Lr} f(t) = f''(t)$. That reminds me of another physical phenomenon, i.e. a mass on a spring which behaves like $a _x= -\omega^2 x$. Can you then work out the solution of the differential equation?

 

[archaic]

@Ayesha02 if you haven't solved differential equations before, then suppose that $f (t)=A\cos (\omega t-B)$ and use the initial conditions I hinted at in a previous post to find the unknowns.

 

[Ayesha02]

@Ayesha02 if you haven't solved differential equations before, then suppose that $f (t)=A\cos (\omega t-B)$ and use the initial conditions I hinted at in a previous post to find the unknowns.

ohh thanks buddy!

 

[Delta2]

@Ayesha02 can you please tell me from which book is this exercise , for me at least it represents a fine blending of electrostatics with circuit theory ,and I just want to know from which book it is.

 

[etotheipi]

@Ayesha02 can you please tell me from which book is this exercise , for me at least it represents a fine blending of electrostatics with circuit theory ,and I just want to know from which book it is.

I agree, it's quite a fun question. Am interested also!

 

[Ayesha02]

Are you guys from India, by any chance?
We have a real tough exam here that we've to appear, and this is one of the questions from our preparatory material.

 

[archaic]

@Ayesha02 can you please tell me from which book is this exercise , for me at least it represents a fine blending of electrostatics with circuit theory ,and I just want to know from which book it is.

Probably from Irodov's problems in general physics or a JEE problems textbook.

 

[rude man]

So
My textbook's solution says that :

angular frequency of the LC oscillation is w=sqrt( 2*pi*$E_0$*R*L)
And that required time is one fourth of time period

Can you explain this please @rude man @archaic

You have written $\epsilon_0$ a wrong way.
I further think you copied wrong because that answer is dimensionally incorrect.
How about you left out a "1/"?
That answer would be correct.

 

[Ayesha02]

You have written $\epsilon_0$ a wrong way.
I further think you copied wrong because that answer is dimensionally incorrect.
How about you left out a "1/"?
That answer would be correct.

yeah i got that...i missed the reciprocal

although, could you help me understand the solution theyve given?

 

[rude man]

yeah i got that...i missed the reciprocal

although, could you help me understand the solution theyve given?

The charge oscillates back and forth between the two spheres at that radian frequency.
The only way you're going to get the answer is by solving the differential equation. There are a number of ways to do that, for example the way a previous poster suggesting a solution of the form $cos(\omega t - \phi)$, $\phi$ a constant.

 

[Ayesha02]

The charge oscillates back and forth between the two spheres at that radian frequency.
The only way you're going to get the answer is by solving the differential equation. There are a number of ways to do that, for example the way a previous poster suggesting a solution of the form $cos(\omega t - \phi)$, $\phi$ a constant.

Ohh finally!
understood:)

 

[archaic]

although, could you help me understand the solution theyve given?

What have you got up until now from solving the differential equation?