- #1
Saladsamurai
- 3,020
- 7
Hello folks 
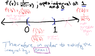
I always thought that inequalities could be treated exactly like equations but somehow I seem to be loosing information or something. For example, if I wish to find all values of x for which the following is true:
1/x + 1/(1-x) > 0
I would 'solve' it as follows
1 + x/(1-x) > 0
x/(1-x) > -1
x > x-1
And here is where I fail. Solving any further results in the obvious: 0>-1.
What is it that I am doing wrong that does not allow me to 'solve' for all x that satisfy the inequality. Am I wrong in thinking that I should be able to.
I always thought that inequalities could be treated exactly like equations but somehow I seem to be loosing information or something. For example, if I wish to find all values of x for which the following is true:
1/x + 1/(1-x) > 0
I would 'solve' it as follows
1 + x/(1-x) > 0
x/(1-x) > -1
x > x-1
And here is where I fail. Solving any further results in the obvious: 0>-1.
What is it that I am doing wrong that does not allow me to 'solve' for all x that satisfy the inequality. Am I wrong in thinking that I should be able to.