Inequality involving a reciprocal - where's the mistake?

[brotherbobby]

Homework Statement

Solve the given inequality : $\boldsymbol{\left( \dfrac{1}{3} \right)^x<9}$

Relevant Equations

1. If $a>b>0\Rightarrow \frac{1}{a}<\frac{1}{b}$
2. If $a<b<0\Rightarrow \frac{1}{a}>\frac{1}{b}$
3. If $a<0<b\Rightarrow \frac{1}{a}<\frac{1}{b}$

(I am not sure how are these relevant. I cannot think of a known rule involving reciprocals and powers. I'd be grateful to be reminded of them).

Problem Statement : Solve the inequality : $\left( \dfrac{1}{3} \right)^x<9$.

Attempts: I copy and paste my attempt below using Autodesk Sketchbook$^{\circledR}$. The two attempts are shown in colours black and blue.

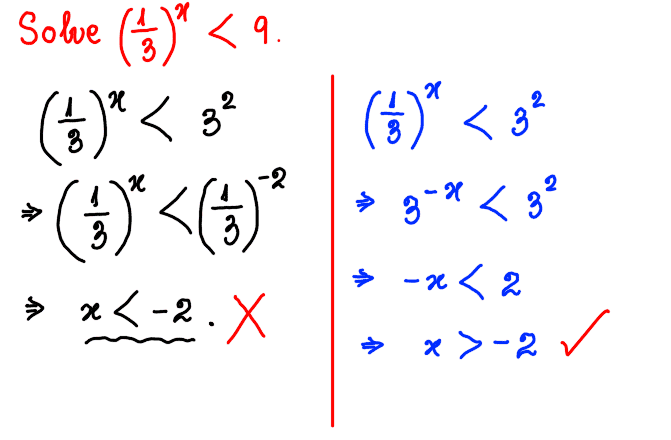
Issue : On checking, the first attempt in black turns out to be incorrect. But I don't understand why.

A hint would be welcome.

 

[BvU]

Hi,
If $0<a<1$ what can you say about $x$ and $y$ when you look at $a^x$ wrt $a^y$ ?

$\$

 

[WWGD]

It seems you could try applying ln or other logs on both sides.

 

[BvU]

Alternative: plot ${1\over 3}^x$

 

[FactChecker]

Powers of fractions less than 1 work differently. Which is larger, $1/3$ or $1/3^2$?

 

[brotherbobby]

Hi,
If $0<a<1$ what can you say about $x$ and $y$ when you look at $a^x$ wrt $a^y$ ?

$\$

Let me take an example. Let $a = \frac{1}{2}$, $x=3$ and $y=4$. We have $\left(\frac{1}{2}\right)^3 = \frac{1}{8}$ and $\left(\frac{1}{2}\right)^4=\frac{1}{16}$. Thus as $x<y$, $a^x>a^y$.

 

[brotherbobby]

It seems you could try applying ln or other logs on both sides.

Let me see.

It solves the problem but doesn't answer my doubt in post# 1 above.

 

[brotherbobby]

Powers of fractions less than 1 work differently. Which is larger, $1/3$ or $1/3^2$?

yes while $3<3^2$, $\frac{1}{3}>\frac{1}{3^2}$

 

[brotherbobby]

Alternative: plot ${1\over 3}^x$

Yes I can see where you getting at. I paste the graph below :

 

[brotherbobby]

I think I have spotted my error. Namely that if $\left(\frac{1}{a}\right)^x<\left(\frac{1}{a}\right)^y\Rightarrow x>y\;\;\forall a>1$.
I correct my error back in post#1 writing below the black ink in green.

 

[PeroK]

It might have been easier to do:
$$\big (\frac 1 3 \big )^x < 9 \Rightarrow \frac 1 {3^x} < 9 \Rightarrow 3^x > \frac 1 9 = 3^{-2} \Rightarrow x > -2$$Notes:
1) $\forall x: 3^x > 0$.

2) $3^x$ is an increasing function.

 

[Mark44]

More succinctly, if a and b are positive,
$\frac 1 a < b \Rightarrow a > \frac 1 b$
Notice the change in direction of the inequality.

 

[WWGD]

To generalize what you, others have said, $x>y$ does not imply $f(x)>f(y)$.