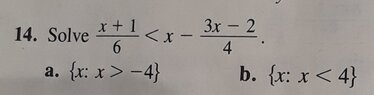Inequality solve (x+1)/6<x-(3x-2)/4

  • MHB
  • Thread starter karush
  • Start date
  • Tags
    Inequality
In summary, the conversation discusses the meaning of "inequality" in a mathematical context and how to solve a given inequality using algebra. It also mentions the purpose of solving inequalities and the specific rules and steps to follow when solving them.
  • #1
karush
Gold Member
MHB
3,269
5
View attachment 9261
Ok a student sent this to me yesterday so want to answer without too many steps

I think the first thing to do is multiply every
term by 12

$2(x+1)<12x-3(3x-2)$
Expanding
$2x+2<12x-9x+6$
 

Attachments

  • Screenshot_20190908-095501_Gallery.jpg
    Screenshot_20190908-095501_Gallery.jpg
    9.1 KB · Views: 90
Last edited:
Mathematics news on Phys.org
  • #2
That’s fine.
 
  • #3
skeeter said:
That’s fine.
$\dfrac{x+1}{6}<x-\dfrac{3x-2}{4}$
Expanding
$2x+2<12x-9x+6$
Combine like terms
$2x+2<3x+6$
Subtract 2x from both sides
$2<x+6$
Subtract 6 from both sides
$-4<x$

Hopefully no typos

Looks like answer a.
 
Last edited:

FAQ: Inequality solve (x+1)/6<x-(3x-2)/4

What is the first step in solving this inequality?

The first step in solving this inequality is to simplify the expressions on both sides of the inequality sign by combining like terms and distributing any coefficients.

How do I determine the critical values for this inequality?

The critical values for this inequality can be found by setting the expressions on both sides of the inequality sign equal to each other and solving for x. These values will divide the number line into different intervals.

Can I multiply or divide both sides of the inequality by a negative number?

Yes, you can multiply or divide both sides of the inequality by a negative number. However, you must remember to flip the direction of the inequality sign when doing so.

How do I graph the solution for this inequality?

To graph the solution for this inequality, plot the critical values on a number line and then determine which intervals satisfy the inequality. The solution will be represented by a shaded region on the number line.

Is there a specific order in which I should solve this inequality?

Yes, when solving an inequality, it is important to follow the order of operations, just like in solving an equation. Simplify the expressions on both sides of the inequality sign first, then isolate the variable on one side of the inequality, and finally, graph the solution and state the solution in interval notation.

Similar threads

MHB Is the solution to the quadratic inequality (-x + 6)/(x - 2) < 0?
Replies
5
Views
1K
MHB Solve Inequality & Simul Eqns: Alg Workings Q (a,b,c)
Replies
1
Views
1K
MHB Equation 2: Prove that ##x^2+2x\sqrt x+3x+2\sqrt x+1=0##
Replies
4
Views
1K
MHB Solve Exponential Equation 4^(5-9x)=1/(8^(x-2) )
Replies
7
Views
3K
MHB Solve √(x^2+3x+7)-√(x^2-3x+9)+2=0
Replies
5
Views
2K
MHB Solve System of Inequalities: 2x+3y-4, 3x-4y+5
Replies
8
Views
1K
MHB Solving $\tan^2x + \tan^2{2x} + \cot^2{3x} = 1$ in R
Replies
6
Views
1K
MHB How do you simplify sqrt{12x^7}?
Replies
2
Views
1K
MHB Solve 2 Equations: 8x-4=9x+6,-x=10
Replies
4
Views
2K
MHB Inequality with fractions solve 2/(x^2−1)≤1/(x+1)
Replies
9
Views
2K

Hot Threads

Recent Insights

Back
Top