I Inertial frames in changing gravitational fields

[Nugatory]

I learned from this thread how referring to the treatment of inertial frames in curved spacetime presents a contradiction of terms, not much different than asking "How does still air behave in a hurricane".

A big and important difference: the behavior of still air is never a good approximation for the behavior of hurricane air, but an inertial frame is an excellent approximation over any small region of spacetime. This is why in general relativity we can speak of local inertial frames, which still work the way we expect, instead of global inertial frames, which do not.
(Although natural language being what it is, people will omit the word “local” when they expect that their audience will understand from the context that it is intended. This leads to great confusion when non-specialists are listening to specialists without understanding this important bit of context).

You could think of general relativity as the way that we relate the local inertial frames that work in one place to the ones that work in another place.

 

[Orodruin]

the behavior of still air is never a good approximation for the behavior of hurricane air,

I would say this depends on the frame and volume extent of the region being described. I would actually say it is a pretty good analogy.

 

[Nugatory]

I would say this depends on the frame and volume extent of the region being described. I would actually say it is a pretty good analogy.

Ah, yes, I wasn’t considering a dust mote moving with the wind... for which the still air approximation is excellent.

 

[jartsa]

Dunno... What do you mean by "affected by time dilation"? A clear answer to that question is also a pretty good hint that there's a better way of thinking about it:

I meant that clocks are slowed down by gravitational time dilation. I forgot that that is wrong, at least according to some people.

Let me try to say it more correctly now. So, large masses are surrounded by a field of curved space-time, which causes observers inside that field to see clocks running extra fast, when they look out through the field.

So when I said that absence of large masses means the absence of gravitational time dilation, that was quite correct. No mass, no field, no gravitational time dilation. Well, except that some distant observer may be looking at a clock that we have placed far from all masses, and that observer may be surrounded by a gravity field. So maybe that part was wrong too.

When I said that next to a large mass there has to be gravitational time dilation, that was wrong. Because observers inside the field do not have to look through the field at a clock, if said clock is right next to them.

I just wonder why an astronaut visiting a planet orbiting a gigantic black hole observes that his buddies have aged a lot, when he gets back up from the planet. He is not looking at those buddies through the field when he is standing next to them.

 

[jbriggs444]

when he gets back up from the planet

Look at @Orodruin's signature. Relativity of simultaneity.

 

[PeterDonis]

I just wonder why an astronaut visiting a planet orbiting a gigantic black hole observes that his buddies have aged a lot, when he gets back up from the planet.

That is not time dilation; that is differential aging. It is accounted for by the simple fact that the astronaut and is buddies took different paths through spacetime, and the former's path was much shorter than the latter's. In other words, it's just geometry. No "slowing down of clocks" is involved--in fact the calculation of differential aging requires that the astronaut's clock ticks at the same "rate" as his buddies', one second per second. The only difference is in the length in seconds of his path through spacetime as compared to theirs.

It's no different from two cars taking two different routes to get from point A to point B, where one route is much shorter than the other. You don't say one car's odometer "slowed down" compared to the other's; both odometers measure one mile per mile. There are just fewer miles in one route than in the other.

 

[bhobba]

I am not sure I follow this part. In which sense does this derive GR. All you will get is Minkowski space in curvilinear coordinates.

That's the point - you are led to a contradiction. You start with flat space-time and end up with the the Lagrangian of GR. Add a matter term to the Lagrangian, vary it and you get the EFE's with the stress energy tensor on one side. Many of the solutions of which are curved space-time. The flat space-time you started with can only be true locally.

Thanks
Bill

 

[Orodruin]

That's the point - you are led to a contradiction.

I do not see where the contradiction is. There is no a priori requirement that the metric is a dynamic field. You just have it expressed in a different set of coordinates. This is no stranger than polar coordinates in the two-dimensional Euclidean plane. Lovelock’s theorem apply only if you assume that the metric is dynamic, the action at most contains second derivatives of the metric, and is linear in those second derivatives. In fact, there are studies of so-called f(R)-theories, where the action is a (not necessarily linear) function of the Ricci scalar.

The flat space-time you started with can only be true locally.

This is only true if you assume all of the above and that the stress-energy tensor is non-zero. Minkowski space is a perfectly fine vacuum solution to the EFEs. However, there is no a priori requirement to make the metric dynamic just because it has a different form in curvilinear coordinates.

 

[bhobba]

This is only true if you assume all of the above and that the stress-energy tensor is non-zero.

You are of course correct. If I gave the impression the assumptions I made are a-priori correct then I explained it badly. Everything you mention is an assumption I made - but a suggestive one to try and get across the idea if you start with an inertial frame and follow a reasonable - but of course assumption laden - line of thought things to not work out correctly - you are led to assuming what you started with was only locally inertial.

I think since it is causing confusion I would have been better giving a different argument based on linearised gravity in an inertial frame as found in Gravitation and Spacetime by O'hanian. Briefly using EM as a guide one can construct linearised gravity in an inertial frame. Then you can show in this theory space-time acts as though it has an infinitesimal curvature. The strange thing is if you assume space-time can have more than just an infinitesimal curvature, which seems quite treasonable, you immediately end up with the full theory of GR. The details can be found in chapter 7 of O'hanians book.

Thanks
Bill

 

[Orodruin]

If I gave the impression the assumptions I made are a-priori correct then I explained it badly.

I think the key word that gave me this impression was ”deriving”. I agree of course that it is a way of making GR plausible. When I teach GR I usually go by the EH action being the simplest non-trivial Lagrangian you can write down and ”oh look! you reproduce Newtonian gravity in the weak field non-relativistic limit and make a ton of other predictions that have been verified to high precision”.

 

[bhobba]

When I teach GR I usually go by the EH action being the simplest non-trivial Lagrangian you can write down and ”oh look! you reproduce Newtonian gravity in the weak field non-relativistic limit and make a ton of other predictions that have been verified to high precision”.

That is an excellent way of doing it.

Thanks
Bill

 

[Android Neox]

The gravitational time dilation at any point in space is determined by the gravitational potential so, as a clock (or observer) moves downward, gravitational time dilation will increase and time will slow. The freely falling observer will have increasing time dilation (slower and slower time) both due to increasing speed (from the perspective of an observer stationary with respect to the massive body) and due to moving to space at lower gravitational potential.

 

[bhobba]

The freely falling observer will have increasing time dilation (slower and slower time) both due to increasing speed (from the perspective of an observer stationary with respect to the massive body) and due to moving to space at lower gravitational potential.

Is there a gravitational field for a freely falling observer?

I think I see what you are saying, but maybe it could be expressed a bit clearer.

Thanks
Bill

 

[Android Neox]

Is there a gravitational field for a freely falling observer?

I think I see what you are saying, but maybe it could be expressed a bit clearer.

Thanks
Bill

I should have been more clear.

No, all observations within the falling observer's frame and local to the observer (e.g. within a falling elevator) would not show any acceleration, gravitational or otherwise. Equivalence Principle holds. However, that's not the determining factor.

Since all correct models & thought experiments are correct (or, at least, not wrong) under all correct interpretations... a single correct thought experiment will yield observations that are logically consistent with those of all observers in all frames.

Thought experiment: Consider a platform, stationary with respect to a Schwarzschild black hole, at some finite coordinate distance above the Schwarzschild radius, $R_s$. On the platform is a winch that can lower a mirror. There is a laser that shines a beam onto the mirror. There is also a device that detects reflected laser light.

At any mirror position along the light beam, it will have some blueshift which follows, exactly, the difference in gravitational potential between the platform and the mirror. The change in time rate exactly follows this, too. If the frequency is doubled, the time rate is halved. That value of time dilation is an attribute of that frame. If the mirror is held stationary with respect to the black hole then that is the frame in which time passes at the maximum rate, for that point in space.

A freely falling observer will also have two other effects that will change the appearance of the light beam: Doppler and relativistic effects of motion with respect to the source.

If it's not clear that the change in laser beam frequency must be the exact inverse of the change in time rate, consider that every light wave cycle that reaches the mirror was first generated at the laser. The light beam is a causal sequence just as falling dominoes are, and so this sequence is the same for all observers in all frames. So, if a lower observer is seeing these wave cycles arriving at twice the rate, they must be measuring time half as fast.

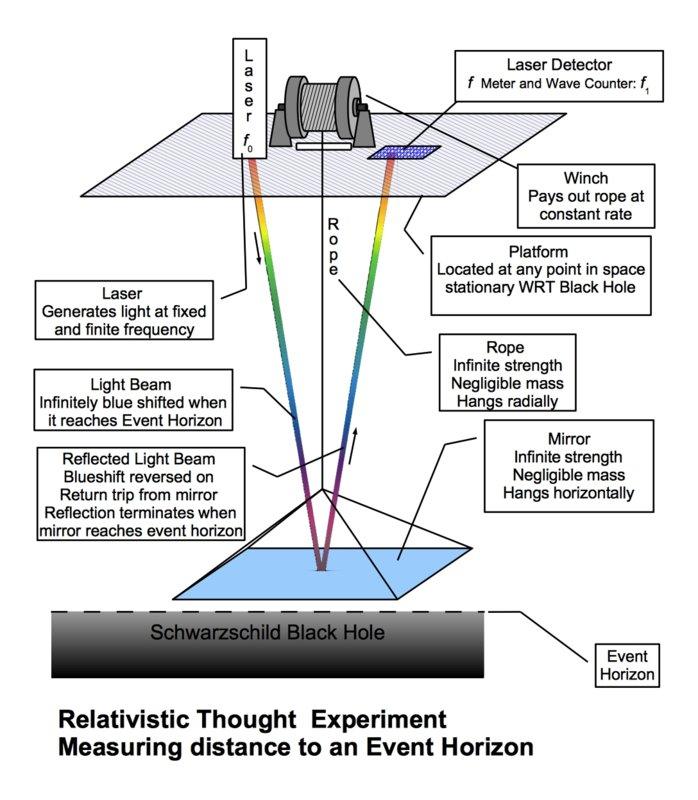
Because the blueshift down to an event horizon, from any point above the EH, is infinite, by the time the front of the beam reaches the event horizon, the beam will be infinitely blueshifted. The beam will contain infinitely many wave cycles. This means that, before the front of the beam can reach the event horizon, infinite time must pass for the light source on the platform. And, since the rope supporting the mirror has been payed out at a constant rate, an infinite amount of rope will be payed out before the front of the light beam could reach the event horizon. Since the mirror is lowered slower than c, it will take event longer than infinite time for the mirror to arrive.

Idealized: All equipment is of infinite strength, negligible mass, and otherwise idealized.

 

[PeterDonis]

at some finite coordinate distance above the Schwarzschild radius

In what coordinates? You appear to be implicitly using Schwarzschild coordinates in the patch exterior to the horizon, but you should not leave that implicit. You should state it explicitly. That way you will be forced to consider the limitations of the coordinates you are using; see further comments below.

At any mirror position along the light beam, it will have some blueshift

Measured by what?

If the mirror is held stationary with respect to the black hole then that is the frame in which time passes at the maximum rate, for that point in space.

"For that point in space" is ambiguous. If you mean "for objects held at that point in space" (and remember, to properly define "point in space" in a coordinate-independent fashion is not trivial, though in this case it can be done), then your statement is vacuous, since only one worldline--path through spacetime--is possible for any such object, and so only one possible rate of time passage is possible.

If, OTOH, you mean "for any objects whose worldlines pass through two selected events, chosen to be at that point in space", then your statement is false. If an observer held stationary along with the mirror throws a clock up in the air vertically, then catches it at some later time, the elapsed time on the clock he threw up will be greater than the elapsed time on the clock he carries with him.

If it's not clear that the change in laser beam frequency must be the exact inverse of the change in time rate

If you mean that the observed redshift/blueshift is exactly proportional to the ratio of gravitational potentials, of course it is. I don't see why you're making such a big deal out of it, since this is a well-known property of stationary observers in Schwarzschild spacetime and has been for decades.

Because the blueshift down to an event horizon, from any point above the EH, is infinite,

Wrong. There are no stationary observers at the EH, nor is it possible to hold the mirror stationary there. So there is no such thing as "the blueshift down to an event horizon", since it's impossible for an observer to exist who could measure it.

before the front of the beam can reach the event horizon, infinite time must pass for the light source on the platform

Wrong. The coordinates you appear to be implicitly using are singular at the horizon, so "infinite time must pass" is not correct because it is attempting to apply coordinates at a coordinate singularity.

since the rope supporting the mirror has been payed out at a constant rate, an infinite amount of rope will be payed out before the front of the light beam could reach the event horizon

Wrong. The proper distance from your laser platform to the mirror, as the mirror gets lowered, approaches a finite limit as the mirror approaches the horizon. (We cannot directly measure such a distance with the mirror at the horizon, since the mirror can't be stationary there, but we can realize the limiting process I have just described by letting the mirror get closer and closer and measuring how the distance varies.)

It looks like you need to read the Insights series on the Schwarzschild geometry:

https://www.physicsforums.com/insights/schwarzschild-geometry-part-1/

You are making a number of elementary errors that are common with people who are not sufficiently familiar with the actual properties of this spacetime geometry.

 

[Android Neox]

It looks like you need to read the Insights series on the Schwarzschild geometry:

https://www.physicsforums.com/insights/schwarzschild-geometry-part-1/

You are making a number of elementary errors that are common with people who are not sufficiently familiar with the actual properties of this spacetime geometry.

Thanks for the response. I'll do that.
I'll probably be back, later, with some new misinterpretations.

 

[bhobba]

I'll probably be back, later, with some new misinterpretations.

Don't worry - that's how you learn.

Thanks
Bill