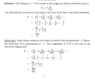Infinite number of identical charges r=a2^n

In summary, the conversation discusses the process of finding the electric field using the formula V=k∑q/r and the relationship between the electric field and potential. The speaker initially assumes that taking the derivative of -V will give the electric field, but realizes that this is not the correct approach. They then mention the concept of taking gradients to find the electric field and acknowledge that the layout of the charges can impact the results.
  • #1
SherlockHolmie
14
1

Homework Statement


xZGequJ.png

Homework Equations


V=k∑q/r
E=-dV/ds

The Attempt at a Solution


I found part A plenty fine, 2kq/a

From here, I thought that the derivative of -V would give me the electric field, giving -2kq/a^2, but that's not the answer according to what my professor sent. I'm wondering why the derivative doesn't work.

21M8nEH.png


I know there's something about how E=-∇V, but I'm not completely sure how to take gradients to begin with, but from my understanding, gradient of a 2d function is just its derivative with respect to its only variable.

Thanks
 

Attachments

  • xZGequJ.png
    xZGequJ.png
    14.9 KB · Views: 511
  • 21M8nEH.png
    21M8nEH.png
    13.5 KB · Views: 397
Physics news on Phys.org
  • #2
SherlockHolmie said:
I thought that the derivative of -V would give me the electric field
The electric field is the derivative of the potential with respect to displacements from the location where you are measuring the potential. That is not the same as a. If you change a you change the whole layout of the charges.
So you need to find the field due to each charge and add those.
 

FAQ: Infinite number of identical charges r=a2^n

1. What is an infinite number of identical charges r=a2^n?

An infinite number of identical charges r=a2^n refers to a hypothetical situation in which there is an infinite number of charges that are all identical and are arranged at equal distances from each other. The distance between each charge is represented by the formula r=a2^n, where a is a constant and n is the number of the charge in the sequence.

2. How is the infinite number of identical charges r=a2^n related to Coulomb's law?

The infinite number of identical charges r=a2^n is related to Coulomb's law, which describes the force of attraction or repulsion between two charges. In this scenario, the force between two charges would follow the same formula as Coulomb's law, but the total force would be the sum of all the individual forces between each charge.

3. Is an infinite number of identical charges r=a2^n possible in reality?

No, an infinite number of identical charges r=a2^n is not possible in reality. This is a theoretical concept used in physics to understand the behavior of charges in a simplified scenario. In reality, there are always a finite number of charges and they are not arranged at equal distances from each other.

4. What implications does an infinite number of identical charges r=a2^n have on electric fields?

An infinite number of identical charges r=a2^n has significant implications on electric fields. It helps to understand the concept of a point charge, which is a theoretical concept used to simplify calculations in electrostatics. It also demonstrates the concept of superposition, where the total electric field at a point is the sum of the electric fields produced by each individual charge.

5. How is an infinite number of identical charges r=a2^n used in practical applications?

An infinite number of identical charges r=a2^n is not used in practical applications as it is a theoretical concept. However, it is used in theoretical models and simulations to understand the behavior of charges in a simplified scenario. It also helps in understanding the concept of electric fields and Coulomb's law, which have many practical applications in areas such as electronics, telecommunications, and energy systems.

Similar threads

Charge on a grounded conducting sphere in a uniform electric field, after ungrounding and movement
Replies
1
Views
753
Understanding Part (b) of a Charge Distribution Problem
Replies
9
Views
1K
Electrostatic Potential Energy stored outside a shell.
Replies
1
Views
4K
Electric field at a point inside a non-uniformly charged sphere
Replies
6
Views
691
What is the magnitude of the field at point R?
Replies
5
Views
1K
Finding electric potential of an infinite line charge at z axis
2
Replies
64
Views
3K
Two charges and electric field?
Replies
4
Views
1K
Charge on a rod of infinite length
Replies
2
Views
2K
Infinite chain of alternating charges (+/-)
Replies
29
Views
3K
Method of mirroring - metal plates
Replies
11
Views
1K

Hot Threads

Recent Insights

Back
Top