member 731016
- Homework Statement
- Pls see below
- Relevant Equations
- Pls see below
For part (b),

The solution is
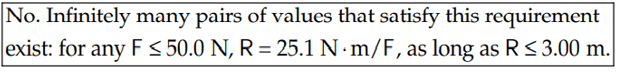
However, is there really an infinite number of pairs physically speaking? It would be very hard, say, vary the force applied by ##0.0000001N## for example.
Many thanks!
The solution is
However, is there really an infinite number of pairs physically speaking? It would be very hard, say, vary the force applied by ##0.0000001N## for example.
Many thanks!