- #1
computerex
- 68
- 0
Hello. I have to solve some integrals using both the standard theorem of calculus and infinite Riemann sums.
[itex] \int_{1}^{7} (x^2-4x+2) dx = \lim_{n \to \infty } \sum f(x_i)\Delta x_i = \lim_{n \to \infty } \sum (x_i^2 - 4x_i + 2)6/n [/itex]
Evaluating the definite integral results in an answer of 30 units.. But it seems I have done something wrong in trying to do it with infinite Riemann sums:
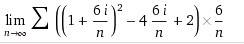
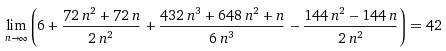
Taking the limit results in 42, not 30. Note I may have prematurely omitted some terms that will evaluate to 0 after taking the limit to save space.. Can someone tell me what I am doing wrong?
[itex] \int_{1}^{7} (x^2-4x+2) dx = \lim_{n \to \infty } \sum f(x_i)\Delta x_i = \lim_{n \to \infty } \sum (x_i^2 - 4x_i + 2)6/n [/itex]
Evaluating the definite integral results in an answer of 30 units.. But it seems I have done something wrong in trying to do it with infinite Riemann sums:
Taking the limit results in 42, not 30. Note I may have prematurely omitted some terms that will evaluate to 0 after taking the limit to save space.. Can someone tell me what I am doing wrong?
Last edited: