Initial velocity and angle when a ball is kicked over a 3m fence

[simphys]

Homework Statement

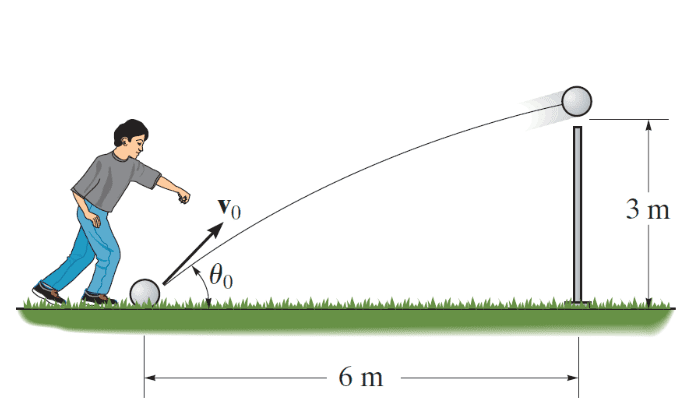
Determine the minimum initial velocity v0 at which the ball must be kicked in order for it to just cross over the 3-m high fence .

Part B:
Determine the corresponding angle $\theta _0$ at which the ball must be kicked.

Relevant Equations

kinematic eqs for constant acceleration

Hello there, I don't understand what I'm doing wrong I don't get the correct answer, but have done the same analysis 3x already and still get the same...

Some input would be appreciated thanks in advance.
Note: y-axis is upwards and x-axis is to the right.

3 unkowns i.e. 3eqs.

$x = x_0 + v_{0,x}t$
$6 = v_0cos\theta * t (1)$

$y = y_0 + v_{0,y}t + \frac 12 a_ct^2$
$3 = v_0sin\theta * t - \frac12 gt^2 (2)$

$v_y = v_{0,y} - gt$
$0 = v_0cos\theta - gt (3)$

$(3) in (2)$ --> $3 = gt^2 - \frac 12 gt^2$
$\frac 12 gt^2 = 3$ --> $t = \sqrt{\frac 6g} = 0.7821s$

$\frac {(3)}{(1)} --> \frac {v_0sin\theta}{v_0cos\theta * t} = \frac {gt}{6}$
$tan\theta = \frac {gt^2}{6}$
$\theta = atan\frac {gt^2}{6}$
$\theta = 45$ degrees --> WRONG

using these result in $(1)$:
$v_0 = \frac {6}{cos\theta * t} = 10.85m/s$ --> also WRONG because of the angle of course.

Thanks in advance.

 

[Orodruin]

Why do you think $45^\circ$ is wrong?

 

[simphys]

Why do you think $45^\circ$ is wrong?

euhh becuase that is what I got as an answer? pulling the intial velocity and angle AND the time as unkowns throught he equations

 

[simphys]

oh @Orodruin because I know the final answers, that is why :)

 

[simphys]

 

[Orodruin]

Well, $45^\circ$ is obviously correct just based on how a parabola looks.

 

[simphys]

Well, $45^\circ$ is obviously correct just based on how a parabola looks.

just as I thought.. but the answers convey a different story unfortunately..
$v_0 = 9.76m/s$ and $\theta = 58.3$ degrees

 

[erobz]

Latex Tip:

You can use Latex code " \to " $\to$ make the arrows, or " \rightarrow " $\rightarrow$. Also, sine " \sin " and cosine "\cos" are special functions that alters the formatting of the text $\sin \theta \, \cos \theta$ . And for units it's better to use " \rm{ \frac{m}{s} } " like $\rm{ \frac{m}{s} }$

 

[Orodruin]

To make that a bit more concrete:

A parabola bending downwards with maximum at $x = 0$ has the shape
$$
y = -ax^2
$$
where $a > 0$. Therefore
$$
y' = -2ax.
$$
This means that at position $-x_0$ the $y$ coordinate is
$$
y_0 = -ax_0^2 \quad \Longrightarrow \quad a = - y_0/x_0^2
$$
and the slope $k = 2ax_0$. Since $\Delta y = y(0) - y(x_0) = -y_0$, the slope is therefore
$$
k = \frac{2\Delta y}{\Delta x} = 1 = \tan\theta_0.
$$

Conclusion: Don't always trust given answers.

 

[simphys]

Latex Tip:

You can use Latex code " \to " $\to$ make the arrows, or " \rightarrow " $\rightarrow$. Also, sine " \sin " and cosine "\cos" are special functions that alters the formatting of the text $\sin \theta \, \cos \theta$ . And for units it's better to use " \rm{ \frac{m}{s} } " like $\rm{ \frac{m}{s} }$

appreciate it! Will def use those next time.

 

[simphys]

To make that a bit more concrete:

A parabola bending downwards with maximum at $x = 0$ has the shape
$$
y = -ax^2
$$
where $a > 0$. Therefore
$$
y' = -2ax.
$$
This means that at position $-x_0$ the $y$ coordinate is
$$
y_0 = -ax_0^2 \quad \Longrightarrow \quad a = - y_0/x_0^2
$$
and the slope $k = 2ax_0$. Since $\Delta y = y(0) - y(x_0) = -y_0$, the slope is therefore
$$
k = \frac{2\Delta y}{\Delta x} = 1 = \tan\theta_0.
$$

Conclusion: Don't always trust given answers.

Thank you, that is interesting. I don't understand how you think in such a way by taking $-x_0$ and stuff, I would never ever do such a thing xD

And thanks for the conclusion, you are right.. good attitude to have to my own answers as well tbh.
But yeah, the thing is that this exercise has probably been done by 600 + students so I kinda assume that all of the answers should be right, no?

 

[simphys]

To make that a bit more concrete:

A parabola bending downwards with maximum at $x = 0$ has the shape
$$
y = -ax^2
$$
where $a > 0$. Therefore
$$
y' = -2ax.
$$
This means that at position $-x_0$ the $y$ coordinate is
$$
y_0 = -ax_0^2 \quad \Longrightarrow \quad a = - y_0/x_0^2
$$
and the slope $k = 2ax_0$. Since $\Delta y = y(0) - y(x_0) = -y_0$, the slope is therefore
$$
k = \frac{2\Delta y}{\Delta x} = 1 = \tan\theta_0.
$$

Conclusion: Don't always trust given answers.

@Orodruin
dudeeeeee... look at this please.. at what he did at 1:40 ... youtube vid
still don't get how this makes my solutions wrong because.. isn't mine the initial velocity as well?

 

[Orodruin]

@Orodruin
dudeeeeee... look at this please.. at what he did at 1:40 ... youtube vid
still don't get how this makes my solutions wrong because.. isn't mine the initial velocity as well?

Your solution is not wrong. At least not for the angle as shown in #9. I have not looked at the initial velocity part.

 

[simphys]

Your solution is not wrong. At least not for the angle as shown in #9. I have not looked at the initial velocity part.

well the question that arises, whether it is correct that this would be the minimum speed I guess then?
forgot to add minimum in the previous post.

like.. how do I know from my solution that it would not be the minimum solution?

 

[Steve4Physics]

Latex Tip:
... And for units it's better to use " \rm{ \frac{m}{s} } " like $\rm{ \frac{m}{s} }$

A bit off-topic, but for information, slightly improved readability of the LaTeX code and to save a tiny amount of work, it's probably worth noting that, for '\frac', if the numerator and/or denominator are single characters, then the curly braces, {}, aren’t needed.

So for example:
\frac m s is rendered as $\frac m s$.
\frac {one} 2 is rendered as $\frac {one} 2$.
\frac 1 {two} is rendered as $\frac 1 {two}$.

 

[erobz]

I think the minimization of the initial velocity was missed?

You need to write $v$ as a function of $\theta$, with parameters $x,y$. Then you need to minimize $v$ using standard optimization techniques from calculus to solve for the angle that minimizes the velocity.

You can reason this out by picking some angle, and initial velocity and see if it makes it over the fence. If you keep decreasing the initial velocity while holding the angle constant, at some point it won't make it over the fence. You have found the minimum velocity that makes it over the fence for the angle you have chosen. Now increase or decrease that chosen angle and repeat process until you find the overall minimum initial velocity (over the set of all valid launch angles). This is basically what the calculus I described above does for you.

 

[Orodruin]

Your solution is not wrong. At least not for the angle as shown in #9. I have not looked at the initial velocity part.

To be more clear. Your solution is the solution that just crosses over the fence when obtaining its maximum height. In order for this to be the minimum velocity required you would need to show that this is indeed the solution that gives the minimal velocity, which you have not argued for.

Edit: Yes, reaching a larger height at any point would require a higher velocity in the y-direction, but it will also require less velocity in the x-direction as the ball will have more time to travel the same x-distance.

 

[jbriggs444]

Yes, reaching a larger height at any point would require a higher velocity in the y-direction, but it will also require less velocity in the x-direction as the ball will have more time to travel the same x-distance.

Suppose, for instance, that we have a one centimeter fence positioned one kilometer away. Will the lowest energy projectile be one that just grazes the top of the fence at a horizontal angle or one that is lobbed at approximately a 45 degree launch angle and reaches a high point about 500.007 meters out?

 

[kuruman]

$v_y = v_{0,y} - gt$
$0 = v_0cos\theta - gt (3)$

I assume that equation (3) in post #1 is supposed to be the minimization condition with respect to angle of the equation just above it. If my assumption is correct, this minimization condition is incorrect. Variable $t$ in the top equation is used as the time flight by OP and is clearly dependent on the projection angle $\theta$. Therefore the correct condition for the extremum should be $0 = v_0cos\theta - g\frac{dt}{d\theta}.$

Be that as it may, the condition for optimizing one of $\Delta x$, $\Delta y$, $v_0$ as the projection angle is varied and two of the other quantities are given is that the velocity at the point of interest (here when passing over the wall) be perpendicular to the initial velocity. That results in a simple expression relating the three quantities that makes each part of this problem a one-liner.

For details see "Projection angle optimization" in https://www.physicsforums.com/insights/how-to-solve-projectile-motion-problems-in-one-or-two-lines/ .

 

[Orodruin]

I will say this though ...
Giving the answer with four significant digits when the input has one significant digit is using waaaay too many significant digits ...

 

[malawi_glenn]

I will say this though ...
Giving the answer with four significant digits when the input has one significant digit is using waaaay too many significant digits ...

yup, fence can be anything between 2.50000000000000000000000000000000000000001 and 3.49999999999999999999999999999999999999999 meters, similar with the distance from the fence...
another poorly constructed physics problem.

 

[Orodruin]

yup, fence can be anything between 2.50000000000000000000000000000000000000001 and 3.49999999999999999999999999999999999999999 meters, similar with the distance from the fence...
another poorly constructed physics problem.

Not as much poorly constructed as poorly answered when answered with four significant digits. The answer should probably just say $60^\circ$.

 

[malawi_glenn]

Not as much poorly constructed as poorly answered when answered with four significant digits. The answer should probably just say $60^\circ$.

Always one student in the class who want to answer questions as "exact" as possible. I even had a kid who wrote the area of a circle with 20 digits just to show he/she had memorized digits of Pi :D

 

[kuruman]

I don't think that this problem is poorly constructed. If the distances were given in terms of $\Delta x$ and $\Delta y$, then there would be no problem in understanding what is being asked and presumably get the answers without additional assumptions and explanations. ("Neglect air resistance" is a tacit assumption.) No problem here.

The sticky point is that the distances are given to 1 sig fig which means that the answer must be given to one (or at most two) sig figs. Still no problem if the answers were graded by a human being who would look at the solution and decide how to mark it based on the derivation and numerical answers. The problem arises when this is graded by a (Turing wannabe) machine that marks as "correct" numerical answers that fall within a globally preset margin of tolerance. When that is the case and to do it right, the AI must be sophisticated enough to look at the input sig figs and adjust the tolerance locally.

When I assigned such machine-graded problems, I preset the tolerance to ±3% and made sure that the random input parameters generated answers within that range when entered to the appropriate number of sig figs as determined by the input. For a 3% preset and an expected answer to 3 sig figs based on the input parameters, that meant no calculated answers less than about 2 in whatever units and powers of 10.

So I think that this problem is poorly administered not poorly constructed. The assigner should have adjusted the input sig figs in the figure to match the ones that were stored as the "correct answer" or marked the answers (him/her)self.

 

[Steve4Physics]

$v_y = v_{0,y} - gt$
$0 = v_0cos\theta - gt (3)$

Hi @simphys. In addition to the excellent guidance already given, I hope this may help...

Your key mistakes in Post #1 are as follows:

In your equation 3 you have used:
$v_{0,y} = v_0cos\theta$
which is incorrect. It should be:
$v_{0,y} = v_0sin\theta$.

Your (incorrect) equation 3 has zero on the left. That shows you have incorrectly assumed the top of the fence corresponds to maximum height of the ball (zero vertical component of velocity, $v_y= 0$).

I guess these errors have combined so that, by accident, you get the correct angle (45º) but perhaps not the correct initial velocity!

 

[kuruman]

Hi @simphys. In addition to the excellent guidance already given, I hope this may help...

Your key mistakes in Post #1 are as follows:

In your equation 3 you have used:
$v_{0,y} = v_0cos\theta$
which is incorrect. It should be:
$v_{0,y} = v_0sin\theta$.

Your (incorrect) equation 3 has zero on the left. That shows you have incorrectly assumed the top of the fence corresponds to maximum height of the ball (zero vertical component of velocity, $v_y= 0$).

I guess these errors have combined so that, by accident, you get the correct angle (45º) but perhaps not the correct initial velocity!

I grappled with this issue for a while while trying to understand OP's equation (3). Then it dawned on me that it is an attempt to find an extremum for $v_{0,y}$ by taking the derivative of the equation above it with respect to $\theta$ and setting the result equal to zero. That's what the zero and $\sin\theta$ are all about in equation (3). However that is the wrong approach because the derivative of the second term, $-gt$ should be $-g\frac{dt}{d\theta}$.

I guess these errors have combined so that, by accident, you get the correct angle (45º) but perhaps not the correct initial velocity!

The correct angle is not 45°, it is $$\theta=\arctan\left[\sqrt{1+\left(\frac{\Delta y}{\Delta x}\right)^2}+\frac{\Delta y}{\Delta x}\right].$$

 

[Steve4Physics]

I grappled with this issue for a while while trying to understand OP's equation (3). Then it dawned on me that it is an attempt to find an extremum for $v_{0,y}$ by taking the derivative of the equation above it with respect to $\theta$ and setting the result equal to zero. That's what the zero and $\sin\theta$ are all about in equation (3). However that is the wrong approach because the derivative of the second term, $-gt$ should be $-g\frac{dt}{d\theta}$.

I too struggled with he OP's working. To me, the simplest explanation was that 2 simple mistakes had been made. Maybe the OP can explain what the intention was.

The correct angle is not 45°, it is $$\theta=\arctan\left[\sqrt{1+\left(\frac{\Delta y}{\Delta x}\right)^2}+\frac{\Delta y}{\Delta x}\right].$$

Ok. I clearly need to think about this some more!

 

[Orodruin]

Ok. I clearly need to think about this some more!

The OP's main problem is assuming that the vertical velocity when passing the fence is zero. If you make this assumption, then the required angle is indeed 45 degrees, but that situation does not correspond to the minimal velocity to pass the fence.

 

[erobz]

I grappled with this issue for a while while trying to understand OP's equation (3). Then it dawned on me that it is an attempt to find an extremum for $v_{0,y}$ by taking the derivative of the equation above it with respect to $\theta$ and setting the result equal to zero. That's what the zero and $\sin\theta$ are all about in equation (3). However that is the wrong approach because the derivative of the second term, $-gt$ should be $-g\frac{dt}{d\theta}$.The correct angle is not 45°, it is $$\theta=\arctan\left[\sqrt{1+\left(\frac{\Delta y}{\Delta x}\right)^2}+\frac{\Delta y}{\Delta x}\right].$$

Well, I suspect they were supposed to get there the long way ( I doubt they are to have this committed to memory in intro physics?), but it's always nice to have the answers to check the math against.

@simphys Hint: leave it as $v^2 = f(\theta)$ and implicitly differentiate. It makes it easier to simplify.

 

[malawi_glenn]

The OP's main problem is assuming that the vertical velocity when passing the fence is zero. If you make this assumption, then the required angle is indeed 45 degrees

This is a classical error in these kind of problems. Not sure why. 45 degrees results in the longest projectile range with a given initial speed given that the starting point and impact is on a horizontal line.

 

[kuruman]

This is a classical error in these kind of problems. Not sure why. 45 degrees results in the longest projectile range with a given initial speed given that the starting point and impact is on a horizontal line.

I think the error is in believing that minimizing the speed is equivalent to minimizing $v_{0y}$ since $v_{0x}$ is constant throughout the trajectory. That is faulty thinking. We want to minimize the sum $\sqrt{v_{0x}^2+v_{0y}^2}$ in a way that will barely put the projectile over the top. The plot below shows the 45° trajectory in blue and the optimized trajectory in orange. The initial speed in the orange trajectory is less than in the blue trajectory.

 

[malawi_glenn]

I think it also has to do with the actual "passing over" phrase. When presented like they were just going to hit a target 6.0 m away from them at a 3.0 m height, the success rate would be higher.

 

[erobz]

@simphys

Here is another fun one to try that will get you thinking about these types of problems:

A projectile is launched (without drag) from $y= 0$ with an initial speed $v$ at some angle $\theta$ where $0 \leq \theta \leq \frac{\pi}{2}$. Determine the equation of the "envelope" $e(x)$ that contains all possible trajectories $y(x)$ as a function of the horizontal distance from the point of launch $x$.

If anyone else replies, please hide your response with the

Spoiler

spoiler function

. Thank you!

 

[berkeman]

@simphys

Here is another fun one to try that will get you thinking about these types of problems:

A projectile is launched (without drag) from $y= 0$ with an initial speed $v$ at some angle $\theta$ where $0 \leq \theta \leq \frac{\pi}{2}$. Determine the equation of the "envelope" $e(x)$ that contains all possible trajectories $y(x)$ as a function of the horizontal distance from the point of launch $x$.

If anyone else replies, please hide your response with the

Spoiler

spoiler function

. Thank you!

@simphys -- If you do want help with this problem posted by @erobz please start a separate thread for it. Thanks.

 

[erobz]

@simphys -- If you do want help with this problem posted by @erobz please start a separate thread for it. Thanks.

Just so I have some better understanding of policy, have I subtly crossed the line? My thought was if they start thinking about this problem (regardless of if they succeed in solving it or not) it would help them understand the HW problem.