Inscribed Angles to Identifying and Understanding

  • Context:
  • Thread starter Thread starter Coder74
  • Start date Start date
  • Tags Tags
    Angles Inscribed
Join the discussion
Registration is free. Ask a follow-up in this thread, or start your own.
Sign up Log in
1 reply · 2K views
Coder74
Messages
20
Reaction score
0
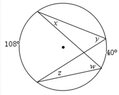
I've been having trouble identifying these inscribed angles for a while. I know the theorem that goes with this topic but I'm unsure how it applies :c.
View attachment 6036
 

Attachments

  • Inscribed Angles.JPG
    Inscribed Angles.JPG
    7.6 KB · Views: 122

Discussion

Mathematics news on Phys.org
Sketch lines out from the centre of the circle to where the points of the inscribed figure meet the circle. Does that help?
 

Similar threads

High School Inscribed Angles: Solve Geometry Problems Easily

  • libbon
  • · Replies 1 ·
  • General Math
Replies
1

Proving Inscribed Angle Theorem for Triangle Side Lengths

  • paulmdrdo1
  • · Replies 5 ·
  • General Math
Replies
5

High School 2 Inscribed Angle Geometry Problems

  • DEMJR
  • · Replies 1 ·
  • General Math
Replies
1

Identifying and understanding random number algorithms

  • schniefen
  • · Replies 2 ·
  • Programming and Computer Science
Replies
2

Angles inscribed in circles part 1

  • grimTesseract
  • · Replies 6 ·
  • Precalculus Mathematics Homework Help
Replies
6

Why are K+ and NO3− spectator ions in Pb(NO3)2 + 2KI precipitation?

  • crybllrd
  • · Replies 2 ·
  • Biology and Chemistry Homework Help
Replies
2

Singular Points of the ODE: Identifying and Understanding

  • cabellos6
  • · Replies 3 ·
  • Calculus and Beyond Homework Help
Replies
3

Redox Reactions: Identifying and Understanding Chemical Transformations

  • nothing123
  • · Replies 1 ·
  • Biology and Chemistry Homework Help
Replies
1