DaveC426913
Gold Member
- 23,915
- 7,958
This comes up in a drafting and illustration contexts. It's a mix of 2D and 3D geometry.
Since I was about twelve and first learning to draw mag wheels on racecars, I've been inscribing circles inside squares.
(Not mine. Stolen off Google)
I noticed right away that it is not as simple as it might seem.
To replicate this, we start with a square, viewed obliquely (1).
Naively inscribing an ellipse into it with its axes aligned to the square's diagonal will result in the incorrect orientation that looks terrible (2).
To seat the circle correctly in the square, the circle must tangentially touch the centre points of all four sides of the square (3). This new shape is also an ellipse, but its major/minor axes are at an angle to the construction lines of the square.
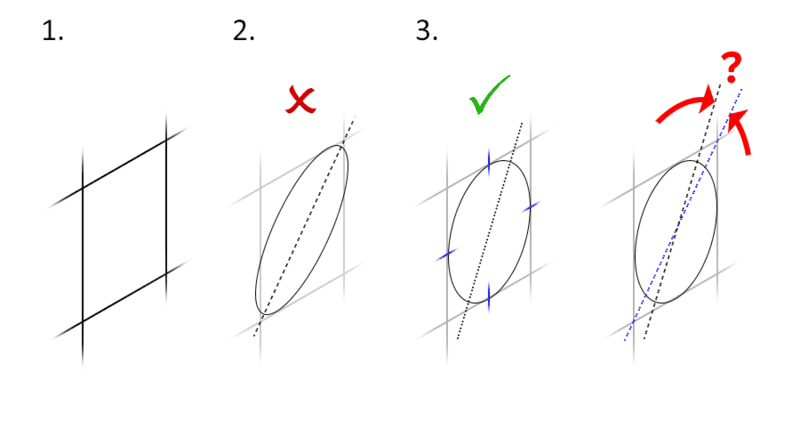
My question is: is there a logic to the relationship between the ellipse's actual axes and the square's construction lines?
(There's other aspects to this question, such as:

 but one thing at a time...)
but one thing at a time...)
Since I was about twelve and first learning to draw mag wheels on racecars, I've been inscribing circles inside squares.
(Not mine. Stolen off Google)
I noticed right away that it is not as simple as it might seem.
To replicate this, we start with a square, viewed obliquely (1).
Naively inscribing an ellipse into it with its axes aligned to the square's diagonal will result in the incorrect orientation that looks terrible (2).
To seat the circle correctly in the square, the circle must tangentially touch the centre points of all four sides of the square (3). This new shape is also an ellipse, but its major/minor axes are at an angle to the construction lines of the square.
My question is: is there a logic to the relationship between the ellipse's actual axes and the square's construction lines?
(There's other aspects to this question, such as:
- how does the relationship hold up when one and two-point perspective is added to the sketch?
- is this relationship related to the patterns on reflective disks?
