- #1
FluidStu
- 26
- 3
The Navier-Stokes equation may be written as:
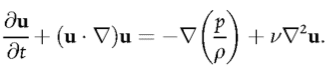
If we have a fixed volume (a so-called control volume) then the integral of throughout V yields, with the help of Gauss' theorem:
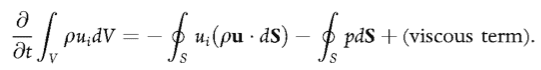
(from 'Turbulence' by Davidson).
The definition of Gauss' theorem:
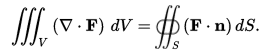
Could someone show me how to go from the integral over the control volume to the closed surface integrals on the left of the second equation? Do we need to use Leibniz's integral rule or Reynolds Transport theorem?
If we have a fixed volume (a so-called control volume) then the integral of throughout V yields, with the help of Gauss' theorem:
(from 'Turbulence' by Davidson).
The definition of Gauss' theorem:
Could someone show me how to go from the integral over the control volume to the closed surface integrals on the left of the second equation? Do we need to use Leibniz's integral rule or Reynolds Transport theorem?