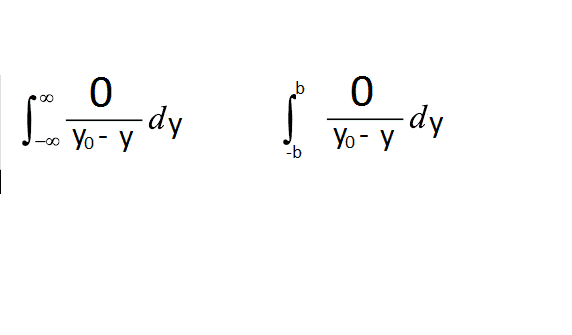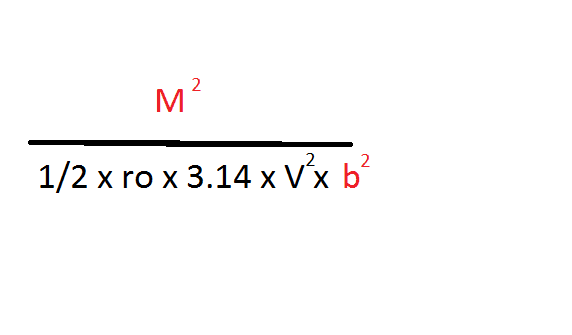I would start with one of your first integrals,
$$\frac 1 {4\pi V}\int_{-b}^b \frac{\frac{d\Gamma}{dy}}{y_0 - y}~dy$$
First, is ##y_0## in the interval [-b, b]? If so, the integral is undefined.
Second, you say that ##\Gamma## (uppercase Greek letter gamma), the circulation, is constant. Since the integral has the derivative of ##\Gamma## in it, that suggests that ##\Gamma## might not be constant.
It would be helpful if you showed where this integral comes from, by posting a photo of the textbook where this integral is discussed.As already mentioned, "ro" should be "rho", the lowercase Greek letter ##\rho##. Density is often represented by ##\rho##.
That makes no sense. You can't just plug in ##\infty## into an expression. In addition, if your logic is correct, you have b being infinitely large as well, so the expression you're trying to evaluate is the indeterminate form ##[\frac \infty \infty]##. I showed three examples earlier in this thread of this type of indeterminate limit, all with different values.