Integral with different variables

[Viona]

Homework Statement

Integral with different variables

Relevant Equations

Integral with variables

I want to do this integral in the picture:

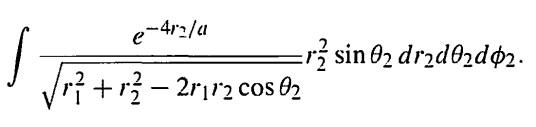
where r1 and a are constants. I know I can integrate each part separately. There will be an integral with respect to r2 multiplied by integral with respect to theta2 and the last one with respect to phi2. But the term under square root confuses me. Can I integrate it with r2 part considering theta2 constant or integate it with theta2 part considering r2 constant?

 

[scottdave]

Yes, see this for more clarification - https://tutorial.math.lamar.edu/Classes/CalcIII/IteratedIntegrals.aspx

Check out the example problems (with solutions)

 

[anuttarasammyak]

Change of variable $t=\cos\theta$ would make
$$\int_{-1}^1 \frac{dt}{\sqrt{A-Bt}}$$
Does it make sense ?

 

[Viona]

Change of variable $t=\cos\theta$ would make
$$\int_{-1}^1 \frac{dt}{\sqrt{A-Bt}}$$
Does it make sense ?

Yes. it seems good. But I want to ask: for this type of integral does the order matter? I should start by integrating w.r.t. r2 first or it is optional?

 

[Viona]

Yes, see this for more clarification - https://tutorial.math.lamar.edu/Classes/CalcIII/IteratedIntegrals.aspx

Check out the example problems (with solutions)

That was helpful. Thanks. I learned that this type of integrals are called iterated integrals. For this type of integral the order is important particularly when the integrand is not continuous on the domain of integration. Then I found a theorem called Fubini’s Theorem. I understood that we can reverse the order if the integrand is continuous on the domain of integration. Now I am wondering how to check if the function is continous or not?

 

[anuttarasammyak]

But I want to ask: for this type of integral does the order matter? I should start by integrating w.r.t. r2 first or it is optional?

Why don' you try integration by $\theta$ at first. The order should not matter for this exercise at least.