Integrate f(x) = tanh(c*x^b)? Wolfram says not possible ....

[mikejm]

I'm working on a guitar amp distortion emulation which is waveshaping based on the following equation:

f(x)= x/|x| * tanh (c * |x|^b)

This looks like this:

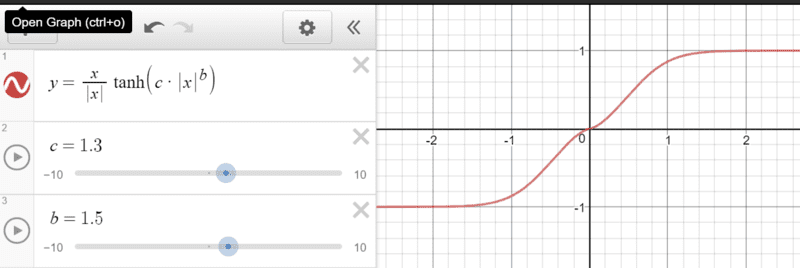
So the idea is values of "x" (the raw guitar signal amplitudes) are fed in and get soft then hard limited to an output of y=+/-1. As the x values approach 0, the exponent "b" shapes them to emulate crossover distortion.

I think it's a nice equation for this type of work.

In order to reduce aliasing (see here), I require the use of the equation's integral.

So I am seeking the integral for this equation, but Wolfram Alpha says that no integral exists. Even for a simplified version:

y= tanh (c*x^b)

It says no such integral exists.

Is this correct? Is there anyway to reorganize the equation or work around it to get a working integral?

Thanks,
Mike

 

[mikejm]

I just thought of something.

The order of operations can be done like:

In which case no special integration of anything is required. I just have to run my "x" values through the (|x|^b*x/|x|) component before multiplying them by drive (c) and then feeding them into my standard tanhx and integrated tanh functions.

Problem solved, I think. :)