Nitacii
- 4
- 0
- Homework Statement
- Calculate the source term ##^2J_{lm}## while knowing by integrating the known quantities.
- Relevant Equations
- $$ ^2J_{lm}(r) = \int_0^{2\pi} \int_0^\pi \frac{(r- i a \cos \theta)^2}{(r_+ - r_-)^2} \Sigma \ J_2 \;{}_{-1}\overline{Y}_{lm} \sin \theta d\theta d \phi$$
Hello, the Homework Statement is quite long, since it includes a lot of equations so I will rather post the as images as to prevent mistypes.
We need to find the integral
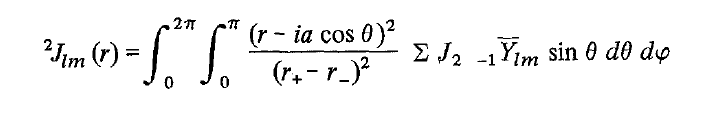
where
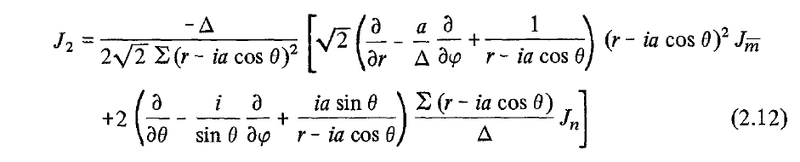
with
$$
J_m =(\sqrt{2}(r−ia\cosθ))^{−1} i(r^2+a^2)\sin(θ)j,
$$
$$
J_n = - \frac{a \Delta}{ 2 \Sigma} \sin(\theta )^2 j,
$$
$$
j = C \delta(r-r_0) \delta(\theta-\pi /2),
$$
where δ is the dirac delta function and with
$$
\Delta = r^2 - 2 M r + a^2
$$
$$
\Sigma = r^2 + a^2 \cos(\theta)^2
$$Finally ##(r_+,r_-,r_0,C,a,M)## are constant and ## {}_{-1}\overline{Y}_{l,m} = {}_{-1}\overline{Y}_{l,m}(\theta,\phi) ## are the Spin-Weighted Spherical harmonics.
We were also given the article Stationary electromagnetic fields around black holes. II. I understand that not everyone has access to it. But I've provided everything necessary here.
Since the calculation are very long I've prepared a Mathematica notebook. Which I've attached as pdf and is also (with working Mathematica notebook) at https://github.com/Zlabekma/homework.git).
Anyway, I don't finish the calculation there because my integrated source term is at least cubic in the variable ##r## but the one in the article is only quadratic in ##r##.
To be more specific in the article they state that ##{}^2J_{lm} \propto \Delta##
Comments on how to improve this post are very much appreciated. Thank you.
We need to find the integral
where
with
$$
J_m =(\sqrt{2}(r−ia\cosθ))^{−1} i(r^2+a^2)\sin(θ)j,
$$
$$
J_n = - \frac{a \Delta}{ 2 \Sigma} \sin(\theta )^2 j,
$$
$$
j = C \delta(r-r_0) \delta(\theta-\pi /2),
$$
where δ is the dirac delta function and with
$$
\Delta = r^2 - 2 M r + a^2
$$
$$
\Sigma = r^2 + a^2 \cos(\theta)^2
$$Finally ##(r_+,r_-,r_0,C,a,M)## are constant and ## {}_{-1}\overline{Y}_{l,m} = {}_{-1}\overline{Y}_{l,m}(\theta,\phi) ## are the Spin-Weighted Spherical harmonics.
We were also given the article Stationary electromagnetic fields around black holes. II. I understand that not everyone has access to it. But I've provided everything necessary here.
Since the calculation are very long I've prepared a Mathematica notebook. Which I've attached as pdf and is also (with working Mathematica notebook) at https://github.com/Zlabekma/homework.git).
Anyway, I don't finish the calculation there because my integrated source term is at least cubic in the variable ##r## but the one in the article is only quadratic in ##r##.
To be more specific in the article they state that ##{}^2J_{lm} \propto \Delta##
Comments on how to improve this post are very much appreciated. Thank you.
Attachments
Last edited: