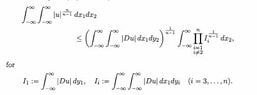Integrating by an other variable

[evinda]

Hello! (Wave)

I am looking at a proof where we have:

$$\int_{-\infty}^{+\infty} |u|^{\frac{n}{n-1}} dx_1 \leq \left( \int_{-\infty}^{+\infty} |Du| dy_1 \right)^{\frac{1}{n-1}} \left( \prod_{i=2}^n \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} |Du| dx_1 dy_i\right)^{\frac{1}{n-1}}$$

Integrating with respect to $x_2$ , I get the following:

$ \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} |u|^{\frac{n}{n-1}} dx_1 dx_2 \leq \left( \int_{-\infty}^{+\infty} |Du| dy_1\right)^{\frac{1}{n-1}} \left( \int_{-\infty}^{+\infty} |Du| dy_2\right)^{\frac{1}{n-1}} \int_{-\infty}^{+\infty} \left( \prod_{i=3}^n \int_{-\infty}^{+\infty} \left( \int_{-\infty}^{+\infty} |Du| dy_i\right) dx_1\right)^{\frac{1}{n-1}} dx_3 $.But according to my notes, we get this:View attachment 5618But it doesn't hold that $ \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} |Du| dx_1 dy_2 = \left( \int_{-\infty}^{+\infty}|Du| dy_1 \right)\left( \int_{-\infty}^{+\infty}|Du| dy_2 \right)$.

Does it ?

Why does the product begin from $1$ and not from $3$? Do we just bound the product I got by the product starting from $1$?

 

[Jhoneine]

No, it does not hold that $\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} |Du| dx_1 dy_2 = \left( \int_{-\infty}^{+\infty}|Du| dy_1 \right)\left( \int_{-\infty}^{+\infty}|Du| dy_2 \right)$. The product begins from $1$ because the integral is taken over the entire domain, so all variables must be included in the product. Therefore, the product should start from $i=1$ and end at $i=n$.