Integrating Different Variables for Work Calculation

[PrashntS]

1. F= 5y i + 6x j (in component form) Find the work done in displacing from (0,0) to (3,4)




2. W= ∫F ds

in this case, W= ∫5y dx + ∫6x dy With lower limits 0,0 And upper Limit 3,4

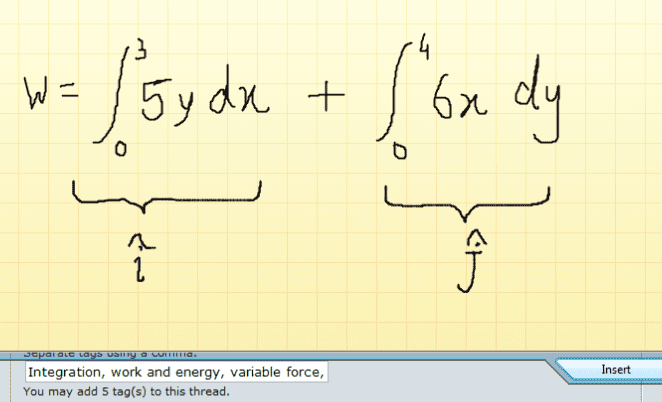
3. Now My question, how do i integrate when variables are different?

 

[HallsofIvy]

x and y are NOT independent. Your integration is on some path (0, 0) to (3, 4). Now the crucial question is whether or not that force vector is "conservative". If it is not, then the work will depend upon the path take, which is not given and it is impossible to find the work done without knowing that path.

If it is, the work done is independent of the path and you can simply choose some simple path to us (the straight line from (0, 0) to (3, 4) or the "broken line" path from (0, 0) to (3, 0) and then to (3,4)). Or you can just find the "potential function" (the function of x and y whose gradient is F) and evaluate it at (0, 0) and (3, 4).

 

[PrashntS]

Yes, that Exactly is the problem i am facing.. I have added picture of my notebook. My teacher had given only that much data... And I think from this data we should assume that path was straight line from (0,0) to (3,4)