Integrating electric field of rod

[member 731016]

Homework Statement

Please see below

Relevant Equations

Please see below

For this problem,

However, I am trying to solve this problem using an alternative method compared with the solutions. My method is:

$\vec E = k_e \int \frac {dq} {r^2} \, dx$ $\hat r$
$\vec E = k_e \int \frac {\lambda} {x^2 + d^2} \, dx$ $\hat r$

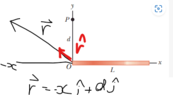
If I let $\hat r = \frac {-x\hat i + d\hat j} {\sqrt {x^2 + d^2}}$ then I get the same answer as the solutions.

However, how dose $\hat r = \frac {-x\hat i + d\hat j} {\sqrt {x^2 + d^2}}$?

I see intuitively that the $\hat r$ dose point in the same direction as the $d\vec E$ for each charge segment $dq$.

Many thanks!

 

[haruspex]

$\vec E = k_e \int \frac {dq} {r^2} \, dx$ $\hat r$

You mean $\vec E = k_e \int \frac {dq} {r^2} \hat r$

dose $\hat r = \frac {-x\hat i + d\hat j} {\sqrt {x^2 + d^2}}$?

Of course. What is the vector from (x,0) to (0,d)?
What is its magnitude?
So what is the unit vector pointing from (x,0) to (0,d)?

 

[member 731016]

You mean $\vec E = k_e \int \frac {dq} {r^2} \hat r$

Of course. What is the vector from (x,0) to (0,d)?
What is its magnitude?
So what is the unit vector pointing from (x,0) to (0,d)?

Thank you for your reply @haruspex ! Yes, thanks for pointing that out: I did mean $\vec E = k_e \int \frac {dq} {r^2} \hat r$.

The vector pointing from (x,0) to (0,d) is $\vec r = -x\hat i + d\hat j$ and its magnitude is $\sqrt{x^2 + d^2}$ so I guess we must divide the $\vec r$ but it's magnitude to find its direction to get $\hat r = \frac {-x\hat i + d\hat j} {\sqrt {x^2 + d^2}}$

Then we just translate the unit vector $\hat r$ to the right for a charge element $dq$ as shown below:

Is my reasoning correct please?

Many thanks!

 

[haruspex]

Thank you for your reply @haruspex ! Yes, thanks for pointing that out: I did mean $\vec E = k_e \int \frac {dq} {r^2} \hat r$.

The vector pointing from (x,0) to (0,d) is $\vec r = -x\hat i + d\hat j$ and its magnitude is $\sqrt{x^2 + d^2}$ so I guess we must divide the $\vec r$ but it's magnitude to find its direction to get $\hat r = \frac {-x\hat i + d\hat j} {\sqrt {x^2 + d^2}}$

Then we just translate the unit vector $\hat r$ to the right for a charge element $dq$ as shown below:View attachment 320665
Is my reasoning correct please?

Many thanks!

Yes.

 

[member 731016]

Yes.

Ok thank you for your help @haruspex !

 

[member 731016]

Thank you for you reply on my other thread @haruspex! That thread has been taken down as I did not realize that I was not allowed to post another thread about another question I had about this problem. In the future I will try to get out all my questions about the same problem in one thread.

So my question was about integrating the y-component of the electric field of the rod. I am not sure how to integrate $E_y = k_ed\lambda\int \frac {dx} {(x^2 + d^2)^{3/2}} \$

Many thanks!

 

[haruspex]

Thank you for you reply on my other thread @haruspex! That thread has been taken down as I did not realize that I was not allowed to post another thread about another question I had about this problem. In the future I will try to get out all my questions about the same problem in one thread.

So my question was about integrating the y-component of the electric field of the rod. I am not sure how to integrate $E_y = k_ed\lambda\int \frac {dx} {(x^2 + d^2)^{3/2}} \$

Many thanks!

There are several ways to proceed.
You can try using a trig substitution to get rid of the square root.
Another way is to turn x.dx into d(x²)/2.
Another is to guess that $(x^2 + d^2)^{1/2}$ may appear in the answer, and differentiate that to see what you get.

Sorry… just realised you are asking about $E_y = k_ed\lambda\int \frac {dx} {(x^2 + d^2)^{3/2}} \$, not $E_y = k_ed\lambda\int \frac {xdx} {(x^2 + d^2)^{3/2}} \$, so the last two won't work.

Bear in mind that (1) an answer in the form of an integral may be acceptable for part a), and (2) part b) asks for an approximation, which suggests that one or both of the integrals cannot be solved exactly.

 

[member 731016]

There are several ways to proceed.
You can try using a trig substitution to get rid of the square root.
Another way is to turn x.dx into d(x²)/2.
Another is to guess that $(x^2 + d^2)^{1/2}$ may appear in the answer, and differentiate that to see what you get.

Sorry… just realised you are asking about $E_y = k_ed\lambda\int \frac {dx} {(x^2 + d^2)^{3/2}} \$, not $E_y = k_ed\lambda\int \frac {xdx} {(x^2 + d^2)^{3/2}} \$, so the last two won't work.

Bear in mind that (1) an answer in the form of an integral may be acceptable for part a), and (2) part b) asks for an approximation, which suggests that one or both of the integrals cannot be solved exactly.

Thank you for your reply @haruspex !

I can solve the first integral for the x-component of the electric field, however, I have not done trig substitution yet.

All the solutions say for the integration of the y-component of the electric field is:

Thank you!

 

[haruspex]

Thank you for your reply @haruspex !

I can solve the first integral for the x-component of the electric field, however, I have not done trig substitution yet.

All the solutions say for the integration of the y-component of the electric field is:
View attachment 320704
Thank you!

You can check that easily enough by differentiating the result.
For trig substitution, what two trig functions do you know that satisfy $g^2=f^2+1$?

 

[member 731016]

You can check that easily enough by differentiating the result.
For trig substitution, what two trig functions do you know that satisfy $g^2=f^2+1$?

Thank you for your reply @haruspex!

There are two trig identities I'm aware of that satisfy $g^2=f^2+1$:

1. $\sec^2\theta = \tan^2\theta + 1$
2. $\csc^2\theta = \cot^2\theta +1$

Which two trig functions were you looking for?

Thank you!

 

[haruspex]

Thank you for your reply @haruspex!

There are two trig identities I'm aware of that satisfy $g^2=f^2+1$:

1. $\sec^2\theta = \tan^2\theta + 1$
2. $\csc^2\theta = \cot^2\theta +1$

Which two trig functions were you looking for?

Thank you!

The first will do. Can you see how to use it to get rid of the square root in the denominator?

 

[member 731016]

The first will do. Can you see how to use it to get rid of the square root in the denominator?

Thanks for your reply @haruspex ! I think so - I'll give it I try!

 

[member 731016]

The first will do. Can you see how to use it to get rid of the square root in the denominator?

So far I have got:

$(\sec^2\theta)^{1/3} = (\tan^2\theta + 1)^{1/3}$
$(\sec\theta)^{2/3} = (\tan^2\theta + 1)^{1/3}$
$\sec\theta = d^2 + x^2$ from comparison
$x = (\sec\theta - d^2)^{1/2}$
$dx = \frac {\sec\theta\tan\theta} {2\sqrt{\sec\theta - d^2}} d\theta$

 

[haruspex]

$\sec\theta = d^2 + x^2$

No, you can't do that. It's dimensionally invalid.
Besides, you want $d^2 + x^2$ to be something squared so that you can take its square root.
Try $x=d\times$ a trig function.

 

[SammyS]

So far I have got:

$(\sec^2\theta)^{1/3} = (\tan^2\theta + 1)^{1/3}$
$(\sec\theta)^{2/3} = (\tan^2\theta + 1)^{1/3}$
$\sec\theta = d^2 + x^2$ from comparison
$x = (\sec\theta - d^2)^{1/2}$
$dx = \frac {\sec\theta\tan\theta} {2\sqrt{\sec\theta - d^2}} d\theta$

Thanks for using LaTeX !

You have some things mixed up. Also, using "d" (lower case D) as a symbol in this problem is a bad idea, but that's what was given to you., so let's go with it.

Actually, you want to let $\displaystyle \tan \theta = \dfrac{x}{(d)}$ , so that $\displaystyle (d) \tan \theta = x$

That gives you $\displaystyle ((d)^2 + x^2)^{(3/2)}=((d)^2 + (d)^2 \tan^2 \theta)^{(3/2)}=(d)^3(1 +\tan^2 \theta)^{(3/2)}$ for your denominator.

The change of variable gives you $\displaystyle dx = (d)\sec^2 \theta \, d\theta$ .

 

[member 731016]

Thanks for using LaTeX !

You have some things mixed up. Also, using "d" (lower case D) as a symbol in this problem is a bad idea, but that's what was given to you., so let's go with it.

Actually, you want to let $\displaystyle \tan \theta = \dfrac{x}{(d)}$ , so that $\displaystyle (d) \tan \theta = x$

That gives you $\displaystyle ((d)^2 + x^2)^{(3/2)}=((d)^2 + (d)^2 \tan^2 \theta)^{(3/2)}=(d)^3(1 +\tan^2 \theta)^{(3/2)}$ for your denominator.

The change of variable gives you $\displaystyle dx = (d)\sec^2 \theta \, d\theta$ .

Sorry for my very late reply - Thank you @haruspex and @SammyS for your replies! I'll see if I can try that out tomorrow, sorry I'm a bit busy at the moment.

No, you can't do that. It's dimensionally invalid.
Besides, you want $d^2 + x^2$ to be something squared so that you can take its square root.
Try $x=d\times$ a trig function.

Also, was it it dimensionally invalid? Is it because there is meters (which dimension is length) on one side and no dimensions on the other side?

Thank you!

 

[haruspex]

Is it because there is meters (which dimension is length) on one side and no dimensions on the other side?

Yes.

 

[member 731016]

Yes.

Thank you @haruspex ! I don't see how you get a conflicting result when you change the units, to cm say. Could you please explain?

Thank you!

 

[member 731016]

Thanks for using LaTeX !

You have some things mixed up. Also, using "d" (lower case D) as a symbol in this problem is a bad idea, but that's what was given to you., so let's go with it.

Actually, you want to let $\displaystyle \tan \theta = \dfrac{x}{(d)}$ , so that $\displaystyle (d) \tan \theta = x$

That gives you $\displaystyle ((d)^2 + x^2)^{(3/2)}=((d)^2 + (d)^2 \tan^2 \theta)^{(3/2)}=(d)^3(1 +\tan^2 \theta)^{(3/2)}$ for your denominator.

The change of variable gives you $\displaystyle dx = (d)\sec^2 \theta \, d\theta$ .

No worries @SammyS ! So solving using trig substitution:

$E_y = k_ed\lambda\int \frac {dx} {(x^2 + d^2)^{3/2}} \$
$E_y = k_ed\lambda\int \frac {(d)\sec^2 \theta \, d\theta} {(d)^3(1 +\tan^2 \theta)^{(3/2)}} \$
$E_y = k_ed\lambda\int \frac {\sec^2 \theta \, \theta} {(d)^2(1 +\tan^2 \theta)^{(3/2)}} \$
$E_y = k_ed\lambda\int \frac {1 +\tan^2 \theta} {(d)^2(1 +\tan^2 \theta)^{(3/2)}} \$
$E_y = k_ed\lambda\int \frac {1} {(d)^2(1 +\tan^2 \theta)^{(1/2)}} \$

I'm not sure how to finish from here. Have I done it correctly so far?

EDITED II: I also found this on an integral table:

However, I think this only holds for when the power of the brackets for the bottom fraction is equal to 1. Am I correct?

Many thanks!

 

[haruspex]

Thank you @haruspex ! I don't see how you get a conflicting result when you change the units, to cm say. Could you please explain?

Thank you!

Suppose d and x are 3cm and 4cm. Your expression in post #13 gives $\sec(\theta)=25$. But putting them in m gives $\sec(\theta)=.00025$.

 

[haruspex]

how to finish from here.

Instead of converting $\sec^2$ to $1+\tan^2$ in the numerator, try the reverse conversion in the denominator.
Btw, you have dropped $d\theta$.

 

[SammyS]

No worries @SammyS ! So solving using trig substitution:

$E_y = k_ed\lambda\int \frac {dx} {(x^2 + d^2)^{3/2}} \$
$E_y = k_ed\lambda\int \frac {(d)\sec^2 \theta \, d\theta} {(d)^3(1 +\tan^2 \theta)^{(3/2)}} \$
$E_y = k_ed\lambda\int \frac {\sec^2 \theta \, \theta} {(d)^2(1 +\tan^2 \theta)^{(3/2)}} \$
$E_y = k_ed\lambda\int \frac {1 +\tan^2 \theta} {(d)^2(1 +\tan^2 \theta)^{(3/2)}} \$
$E_y = k_ed\lambda\int \frac {1} {(d)^2(1 +\tan^2 \theta)^{(1/2)}} \$

I'm not sure how to finish from here. Have I done it correctly so far?

EDITED: I also found this on an integral table:
View attachment 321000
However, I think this only holds for when the power of the brackets for the bottom fraction is equal to 1.

Change $\displaystyle 1+ \tan^2 \theta$ to $\displaystyle \sec^2 \theta$ rather than the other way around. Pull the $\dfrac 1 {(d)^2}$ out of the integral. Also, you have somehow dropped the $d\theta$ from the integral. (maybe a typo)

 

[member 731016]

Suppose d and x are 3cm and 4cm. Your expression in post #13 gives $\sec(\theta)=25$. But putting them in m gives $\sec(\theta)=.00025$.

Thank you @haruspex for the example - I see now!

 

[member 731016]

Thank you for your replies @SammyS and @haruspex ! Sorry it dose look like I dropped the $d\theta$

$E_y = k_ed\lambda\int \frac {\sec^2 \theta \, d\theta} {(d)^2(sec^2 \theta)^{(3/2)}} \$
$E_y = k_ed^{-1}\lambda\int \frac {\sec^2 \theta \, d\theta} {(sec \theta)^3} \$
$E_y = k_ed^{-1}\lambda\int \frac {1} {(sec \theta)} \, d\theta$
$E_y = k_ed^{-1}\lambda\int cos\theta \, d\theta$
$E_y = k_ed^{-1}\lambda sin\theta$

Is it so far correct? I should probably add some limits of integration e.g $\theta_1 = 0$ and $\theta_2 = 90$

 

[SammyS]

Thank you for your replies @SammyS and @haruspex ! Sorry it dose look like I dropped the $d\theta$

$E_y = k_ed\lambda\int \frac {\sec^2 \theta \, d\theta} {(d)^2(sec^2 \theta)^{(3/2)}} \$
$E_y = k_ed^{-1}\lambda\int \frac {\sec^2 \theta \, d\theta} {(\sec \theta)^3} \$
$E_y = k_ed^{-1}\lambda\int \frac {1} {(\sec \theta)} \, d\theta$
$E_y = k_ed^{-1}\lambda\int \cos\theta \, d\theta$
$E_y = k_ed^{-1}\lambda \sin\theta$

Is it so far correct? I should probably add some limits of integration e.g $\theta_1 = 0$ and $\theta_2 = 90$

Not the correct limits of integration.
You can write $\sin \theta$ in terms of $x$ and integrate from $0$ to $L$, the original limits of integration.
Or you can find the limits of integration you need for $\theta$.

 

[member 731016]

Not the correct limits of integration.
You can write $\sin \theta$ in terms of $x$ and integrate from $0$ to $L$, the original limits of integration.
Or you can find the limits of integration you need for $\theta$.

Thank you for you reply @SammyS !

$E_y = k_ed^{-1}\lambda\int_0^{\theta_L} cos\theta \, d\theta$
$E_y = k_ed^{-1}\lambda sin\theta_L$

Where $\theta_L$ is the angle the position vector makes with in the $-\hat j$ direction to the end of the rod.

$E_y = k_e\lambda \frac {L} {d(L^2 + d^2)^{1/2}}$
$E_y = \frac {k_eQ} {d(L^2 + d^2)^{1/2}}$

Which is the same answer as the solutions! :)