Integrating pressure over area to get friction force

[Ortix]

I'm doing some experiments where I need to calculate the resistance force on a cylindrical body (cable) when it's being pulled through water saturated sand

We derived formula from a theory which was originally based on a square body by using stress components. This way we know the pressure at any given depth on the cable.

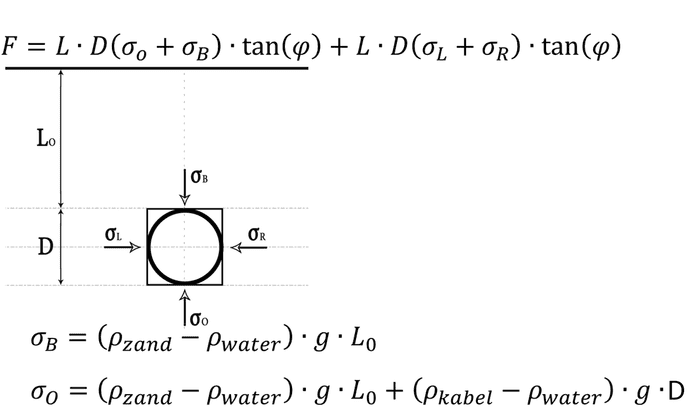
This depicts a square body under sand saturated in water.
(It's in dutch but I'm sure we all can figure out what zand and kabel mean ;) )

The formula we derived (which is a bit too big to put here) was put into MATLAB and this is where it breaks down. 2 other guys from my team calculate the resistance force like so (quick sample code):

for theta = 0:0.1:360
    sigma_point(i) = sigma(theta); // sigma is the formula as a function of theta. Theta is converted to rads
    i = i+1;
end

force = sum(sigma_point)/length(sigma_point)*area_of_cable*coeff_fric

What they do is they calculate the pressure/stress on each point of the 2D-surface with steps of 0.1 degrees. They sum that and divide that by the amount of steps they have taken. Finally they multiply it by the area of the cable and the coefficient of friction which is tan(phi), also known as the angle of friction.

But I'm not buying this. It just doesn't make sense to me. Every fiber in my body is screaming that we should integrate over the area to get the force immediately. I tried it but I'm getting forces in ranges of kilo Newtons which doesn't make sense.

What I did was (i can't get formulas to work):

1. integral from 0 to 2pi of sigma(theta)*radius*length*d_theta
2. multiplied the above result with the coefficient of friction.

I hope I was clear enough because I'm confusing myself here as well.
My question is basically whether the first MATLAB approach is correct and if not what would be a correct way to calculate the friction force.

I'll gladly supply more information/explanation if necessary

 

[mfb]

Why do you subtract densities of sand and water? I would expect a weighted average here.

Every fiber in my body is screaming that we should integrate over the area to get the force immediately.

That's what they are doing, numerically. It is not necessary, however. Pressure increases linearly with depth. The average pressure is just the pressure at the middle of the cable - assuming it does not move upwards or downwards through the sand too fast.