Integrating to find the electric field

[SchruteBucks]

Homework Statement

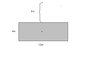
The picture attached shows an insulated board (12m x 4m) with uniform charge density σ. Integrate to find the electric field 8 cm above the center of the board.

Homework Equations

I found the equations \vec{E}=\int\frac{kdq}{r^{2}}\hat{r} and dq=σdy (both from google)

The Attempt at a Solution

We've never integrated to find anything in this class before so forgive my crude attempt...
I ended up with k\int^{10}_{6}\frac{σdy}{y^{2}}(-\hat{j})

I didn't put anything relating to the width of the board because I'm assuming its part of the density, with σ=Q/V=Q/48m²

Any help would be VERY much appreciated

 

[Spinnor]

Don't you need a double integral? Also won't dq = σdxdy?

 

[SchruteBucks]

Sorry, I should've mentioned that my prof. says that the "symmetry of the situation means only one is needed." As far as if dq=σdxdy, I'm assuming it's just σdy since it's only supposed to be a single integral, but in all honesty, I have no idea. Maybe the other integral isn't needed since we already know the area of the board...?

This is my first time setting up an integral for an electric field, and the only equation I have is the one above, though looking at it now, it looks like it's an equation for a one-dimensional object.

I think I'm more confused now.

 

[Spinnor]

If you knew the electric field due to a line of charge then you could turn this into a one dimensional integral. σ is charge per area so you need to multiply by an area, dxdy, to get charge. I might be missing something here, hopefully others will reply.