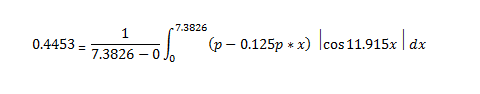Integration by parts with absolute function

In summary, the conversation is about calculating the average value of a function between certain limits, specifically the value of p. The person has provided the equation they need to solve, but is struggling due to the use of Latex commands and the absolute value of cos. Another person suggests using a CAS and provides the solution of p being approximately 17812/13715. The first person asks for an explanation of how this solution was reached and if there is a general formula or steps that can be followed.
  • #1
Mathboi1
2
0
Hi all,

I have the average value of a function between limits of 7.3826 and 0 which equals 0.4453. I have used the formula for average value function and attached the equation I need solving as I don't know how to use the Latex commands. P is what I am trying to work out. Unfortunately I have been unsuccessful since the absolute of cos makes this difficult. If anyone can solve this with working solution I'd be very grateful as I've spent all day trying to solve it.

View attachment 5087

Cheers,

Mathsboi
 

Attachments

  • power equation.png
    power equation.png
    1.5 KB · Views: 76
Physics news on Phys.org
  • #2
Using a CAS, I get:

\(\displaystyle p\approx\frac{17812}{13715}\)
 
  • #3
MarkFL said:
Using a CAS, I get:

\(\displaystyle p\approx\frac{17812}{13715}\)

Thanks for responding,

Can you please explain how you got here? I need to find p with different values of the LHS value and 0.125, keeping everything else the same. Is there a general formula I could use or can you show me steps to your solution?
 
Last edited:
  • #4
Factor $p$ out of the integrand.
 

FAQ: Integration by parts with absolute function

What is Integration by Parts with Absolute Function?

Integration by Parts with Absolute Function is a mathematical technique used to solve integrals involving absolute values. It involves breaking down a complex integral into simpler parts and using the properties of absolute values to solve it.

When is Integration by Parts with Absolute Function used?

Integration by Parts with Absolute Function is used when solving integrals that involve a product of two functions, one of which is an absolute value function. It is also used when the integrand contains a variable within an absolute value.

How do you solve an integral using Integration by Parts with Absolute Function?

To solve an integral using Integration by Parts with Absolute Function, we follow the formula: ∫f(x)|g(x)| dx = f(x)∫|g(x)| dx - ∫f(x)g'(x)sgn(g(x)) dx, where sgn(g(x)) is the sign function of g(x). We then use integration by parts on the second term to further simplify the integral.

What are the benefits of using Integration by Parts with Absolute Function?

Integration by Parts with Absolute Function allows us to solve integrals that may not be solvable using other integration techniques. It also helps in simplifying complex integrals and makes the integration process more efficient.

Are there any limitations to using Integration by Parts with Absolute Function?

Integration by Parts with Absolute Function may not always lead to a solution, especially if the integral contains multiple absolute value terms. It also requires a good understanding of integration by parts and the properties of absolute values to successfully solve integrals using this method.

Similar threads

I Did Math DF's integral calculator make a glaring mistake?
Replies
8
Views
1K
B Why don't we account for the constant in integration by parts?
Replies
16
Views
3K
MHB Visualization of Integration by Parts
Replies
4
Views
2K
B Integral of cosecant function: understanding different approaches
Replies
14
Views
2K
B Are there mathematicians that dislike integral calculus?
Replies
15
Views
3K
B Are Both Answers Correct for Trigonometric Substitution Integral?
Replies
5
Views
2K
Definite integral of an absolute value function
Replies
1
Views
1K
MHB What is the Absolute Maximum Value of f in the Function f(x) = ln(x)/x?
Replies
5
Views
2K
A Integral of 2 Bessel functions of different orders
Replies
3
Views
2K
B Finding Multiple Ways to Integrate
Replies
5
Views
2K

Hot Threads

Recent Insights

Back
Top