- #1
wirefree
- 108
- 21
I greatly appreciate this chance to submit a query.
I have the following integral: $$\int_{1}^t 2sin(t-\tau)e^{-2(t-1)} d\tau$$
and it has been suggested to me that if I sketch the two constituent functions and multiply them, I can read the answer off the paper. So here are my sketches: go straight to the 3rd arrow
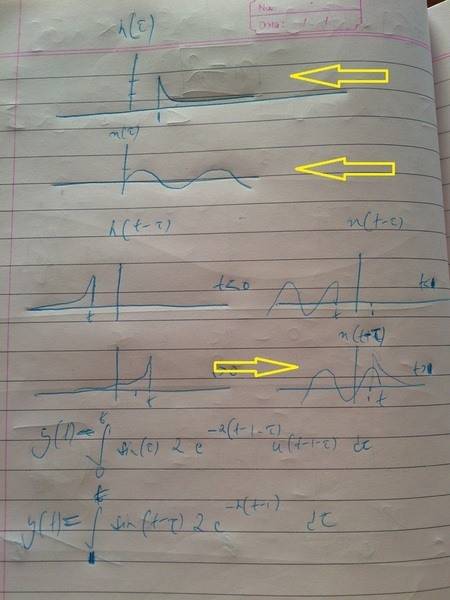
Don't let alternative integral side-track you; it involves something called "convolution" and is something I am grappling with too.
My firtst attempt: There is clearly some area under the graphs, so the answer is not 0. The alternatives I have are: 0, 1 or 2. But, surely, that's not something I can read that off the graph?
My second attempt: I just did the integral by taking $$2e^{-2(t-1)}$$ out; but that simply integrates down to an expression in terms of 't', and without any value of 't' I can't see how a definite answer can be obtained.
Any assistance with tackling the above would be helpful I am sure. Your advice is sought.wirefree
I have the following integral: $$\int_{1}^t 2sin(t-\tau)e^{-2(t-1)} d\tau$$
and it has been suggested to me that if I sketch the two constituent functions and multiply them, I can read the answer off the paper. So here are my sketches: go straight to the 3rd arrow
Don't let alternative integral side-track you; it involves something called "convolution" and is something I am grappling with too.
My firtst attempt: There is clearly some area under the graphs, so the answer is not 0. The alternatives I have are: 0, 1 or 2. But, surely, that's not something I can read that off the graph?
My second attempt: I just did the integral by taking $$2e^{-2(t-1)}$$ out; but that simply integrates down to an expression in terms of 't', and without any value of 't' I can't see how a definite answer can be obtained.
Any assistance with tackling the above would be helpful I am sure. Your advice is sought.wirefree