tent
- 17
- 2
- Homework Statement
- I give a particle a circular trajectory at 2 units of distance from the origin, and an angular velocity of 4 rad/s, both constant. Then I derive the velocity to obtain the radial acceleration, -32. I then say, "Given -32 radial acceleration, can I obtain the original position vector with the appropriate initial conditions?"
- Relevant Equations
- Acceleration, velocity, position components in polar coordinates
I made this exercise up to acquire more skill with polar coordinates. The idea is you're given the acceleration vector and have to find the position vector corresponding to it, working in reverse of the image.
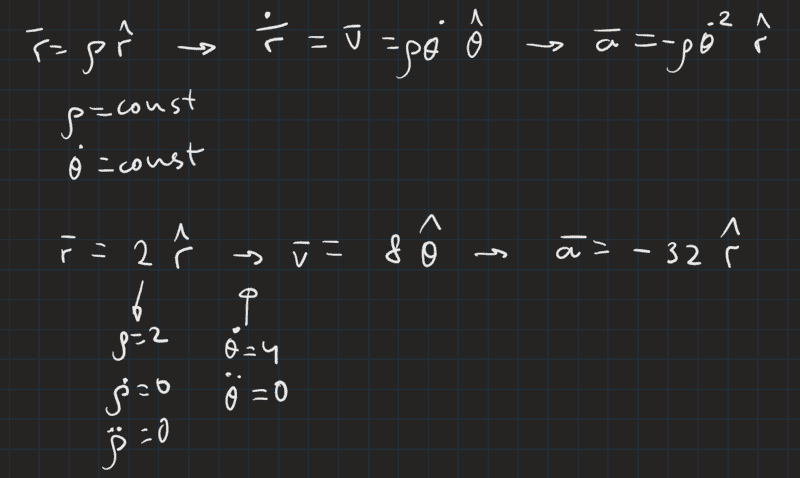
My attempts are the following, I proceed using 3 "independent" methods just as you would solve a Cartesian coordinates kinematic problem, by integrating the acceleration.
1) From the radial and angular acceleration, a system of 2 diff eqs. Integrating by parts the angular one.
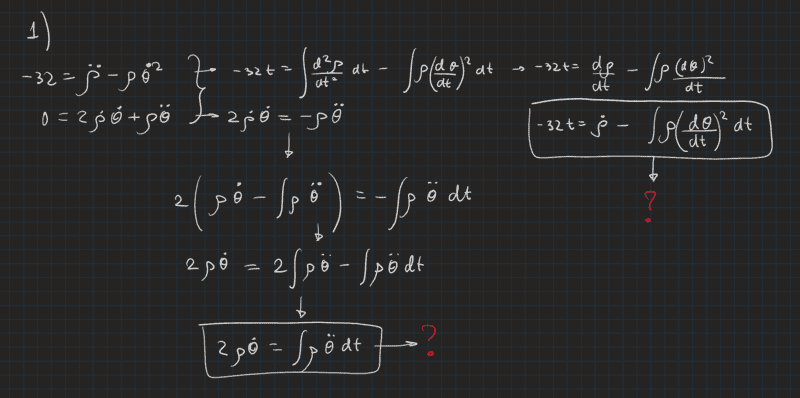
2) Then, by Cartesian subsitution.
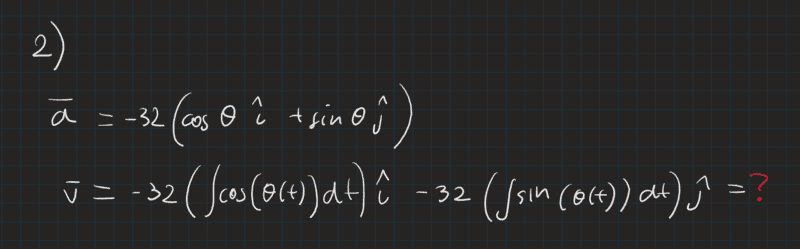
3) Finally by integrating the radial unit vector.
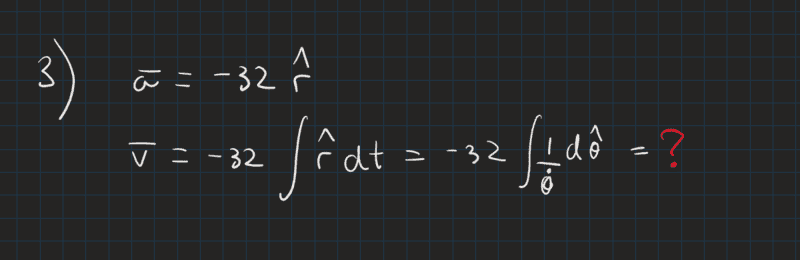
Everything seems impossible to integrate and I'm out of ideas. The initial conditions are irrelevant, though I'm aware you could probably deduce that this is a circular motion from them, and hence solve this easily. The point is to generalize this simple example to an acceleration of an arbitrary trajectory with both components where you shouldn't be able to heuristically deduce the velocity or position. However, I can't even solve this seemingly trivial case.
My attempts are the following, I proceed using 3 "independent" methods just as you would solve a Cartesian coordinates kinematic problem, by integrating the acceleration.
1) From the radial and angular acceleration, a system of 2 diff eqs. Integrating by parts the angular one.
2) Then, by Cartesian subsitution.
3) Finally by integrating the radial unit vector.
Everything seems impossible to integrate and I'm out of ideas. The initial conditions are irrelevant, though I'm aware you could probably deduce that this is a circular motion from them, and hence solve this easily. The point is to generalize this simple example to an acceleration of an arbitrary trajectory with both components where you shouldn't be able to heuristically deduce the velocity or position. However, I can't even solve this seemingly trivial case.
Last edited: