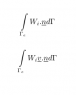Integration of the dot product of two vectors

[hoomanya]

Hi,

I am having problems understanding the difference between the equations in the files attached profile2.png. where W_i is just representing the ith component of the variable W, and n and v under bars are two vectors, and gamma is a boundary and gamma_e shows is a boundary.

what confuses me the most is the presence of the dot.

Any help would be appreciated very much.

Thanks,

 

[HallsofIvy]

If $W_i$ is the ith component of the vector W, then the first one simply makes no sense. You cannot have a dot product of a number and a vector.
$$\int_{\Gamma_e} \vec{W}\cdot \vec{n} d\Gamma$$
would make sense.

What the second one means depends upon what the vector v is.

 

[hoomanya]

Thanks. Ok ! Can you please tell me what a dot product of two vectors gives you? A scalor or a vector? and what that means physically?

Also would the second equation make sense if it was W_i was a vector?

 

[homology]

The basic idea of something like $$\vec{u}\cdot \vec{v}$$ is that it gives you the amount of u in the direction of v, times the magnitude of v. So a classic example is work $$W=\vec{F}\cdot\vec{x}$$ which gives you the amount of force in the direction of displacement x, times the amount of displacement (magnitude of x).

Do you want to know how to calculate it? Have you looked at the wikipedia page yet? Does that make sense or no?

 

[HallsofIvy]

The dot product of two vectors, by definition, is a scalar.

 

[hoomanya]

Thanks for you answers. Wikipedia made sense also. :)