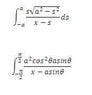- #1
dollarbills10
- 3
- 0
Hi,
I am seeking some input for an integral I have been stumped on for a few days.
This is the integral:
[(a^2 - s^2)^1/2]/(x-s) ds evaluated over the bounds from -a to a. The symmetry of the integration area allows the integral to be evaluated from 0 to a, and doubled.
I have always been conditioned to use trig substitution for an integral when an expression such as (or usually, exactly as) (a^2 - s^2)^1/2 is in the integrand. However, this is unique in that this expression is being divided by x-s in the integrand.
Any suggestions?
Thank you in advance, I am new so I apologize if I have not presented my topic in the most ideal format.
I am seeking some input for an integral I have been stumped on for a few days.
This is the integral:
[(a^2 - s^2)^1/2]/(x-s) ds evaluated over the bounds from -a to a. The symmetry of the integration area allows the integral to be evaluated from 0 to a, and doubled.
I have always been conditioned to use trig substitution for an integral when an expression such as (or usually, exactly as) (a^2 - s^2)^1/2 is in the integrand. However, this is unique in that this expression is being divided by x-s in the integrand.
Any suggestions?
Thank you in advance, I am new so I apologize if I have not presented my topic in the most ideal format.