warhammer
- 164
- 33
- Homework Statement
- Amplitudes of light coming from coherent sources (say 1 and 3 with their units) are different. One has an amplitude 3 times more than the other. Plot the intensity distribution of the resulting wave.
- Relevant Equations
- Intensity ~ (Amplitude)^2
Intensity I=I(1)+I(2) +2√(I(1)*I(2))*cosΦ where Φ=Phase Difference
We assume incident waves to be:
y(1)=y(o)sin(wt)
y(2)=3y(o)sin(wt+Φ)
As Intensity~(Amplitude)^2
We get y(2)=3y(1)
This gives us I(2)=9I(1)
We assume I(1)=I(o) & I(2)=9I(o)
Resultant Wave Intensity I=I(1)+I(2) +2√(I(1)*I(2))*cosΦ ---->
I(o) + 9I(o) + 6I(o)cosΦ (We can take cos of this angle=1 for coherent sources)
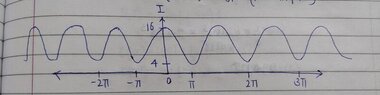
This gives us I=16I(o)
Thus I(max) = {y(1)+3y(1)}^2= 16y(1)^2
I(min)={3y(1)-y(1)}^2= 4y(1)^2
(A Rough representation of the Plot Distribution is attached below).
I request someone to please guide if my approach and solution are correct/incorrect
y(1)=y(o)sin(wt)
y(2)=3y(o)sin(wt+Φ)
As Intensity~(Amplitude)^2
We get y(2)=3y(1)
This gives us I(2)=9I(1)
We assume I(1)=I(o) & I(2)=9I(o)
Resultant Wave Intensity I=I(1)+I(2) +2√(I(1)*I(2))*cosΦ ---->
I(o) + 9I(o) + 6I(o)cosΦ (We can take cos of this angle=1 for coherent sources)
This gives us I=16I(o)
Thus I(max) = {y(1)+3y(1)}^2= 16y(1)^2
I(min)={3y(1)-y(1)}^2= 4y(1)^2
(A Rough representation of the Plot Distribution is attached below).
I request someone to please guide if my approach and solution are correct/incorrect
Attachments
Last edited: