Intensity of a laser beam at a certain distance

[lorenz0]

Homework Statement

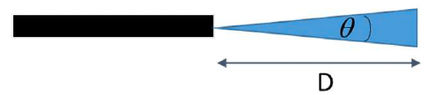
A laser emits radiation of wavelength $\lambda= 632.8 nm$ and a power of $3 mW$ and its beam has an angular divergence equal to $180 \mu rad$. What is the intensity of the laser beam at a distance of $D = 5 m$?
What would be the power of an isotropic source that provided the same intensity at the same distance?

Relevant Equations

$\theta=\frac{2R}{D}$, $I=\frac{P}{4\pi d^2}$

I haven't been able to pinpoint a definition of "angular divergence" of a laser so by pure intuition I assumed it would be something like $\theta=\frac{2R}{D}$ and with that I have that the radius of the lase beam is $R=\frac{D\theta}{2}=90\cdot 5 \cdot 10^{-6} m=450\ \mu m$ so $I_{5m}=\frac{P}{4\pi R^2}=\frac{3\cdot 10^{-3}}{4\pi \cdot 450^2 \cdot 10^{-12}}\simeq 1179\ \frac{Watt}{m^{2}}$ and so I get for an isotropic source $P_{iso}=I_{5m}\cdot 4\pi D^2=1179\cdot 4\pi 5^2 Watt=370391 Watt$. Now, I am suspicious of these results since I never had to use the wavelength \lambda so I think my definition of angular divergence is wrong; could anyone shed some light on this definition and how to apply it in this case? Thank you very much.

 

[BvU]

Hi,

A simple google would have shown your intuition is almost OK...

And checking your math is always a good idea $$R=\frac{D\theta}{2}=90\cdot 5 \cdot 10^{-6} \ {\sf m}=450\ {\sf nm}\quad ?$$

$\$

 

[BvU]

Checking dimensions is always a good idea too $$I=\frac{I}{4\pi D^2}=\frac{3\cdot 10^{-3}}{4\pi 5^2}\ {\sf W}\simeq 9.6\cdot 10^{-6}\ {\sf W}\qquad ?$$

More tips: don't use $I$ and $I$ if $I\ne I$ !

$\$

 

[lorenz0]

Hi,

A simple google would have shown your intuition is almost OK...

And checking your math is always a good idea $$R=\frac{D\theta}{2}=90\cdot 5 \cdot 10^{-6} \ {\sf m}=450\ {\sf nm}\quad ?$$

$\$

What I meant by "I haven't been able to pinpoint a definition" is that I found several definitions and since I didn't know the correct one to use in this case I went with the one that intuitively made the most sense.
------
Still, I don't understand why the problem gives $\lambda$ if it is of no use in the solution.

 

[haruspex]

so I get for an isotropic source $I=\frac{P}{4\pi D^2}=\frac{3\cdot 10^{-3}}{4\pi 5^2}\ \frac{Watt}{m^2}\simeq 9.6\cdot 10^{-6}\ \frac{Watt}{m^2}$.

I don't understand this calculation. You seem to have found the intensity ($Wm^{-2}$, not $W$) that would have been obtained with the same power source had it been isotropic. That is not what you are asked to find.

 

[BvU]

I found several definitions

In such a case, (i.e. if your notes or textbook don't provide one) you state the definition and work with that, as you did. If I were to grade it (and notes or textbook indeed don't provide one), I wouldn't subtract points.

And the first hit (gentec) agrees with your intution, so my 'almost' was in error !

 

[BvU]

Now on to $$I_{5m}=\frac{P}{4\pi R^2}$$This is for an isotropic source. But not for your laser!

 

[lorenz0]

I don't understand this calculation. You seem to have found the intensity ($Wm^{-2}$, not $W$) that would have been obtained with the same power source had it been isotropic. That is not what you are asked to find.

Thanks, it should be correct now.

 

[haruspex]

Now on to $$I_{5m}=\frac{P}{4\pi R^2}$$This is for an isotropic source. But not for your laser!

That R is not the distance from the source. D is used for that here.

 

[lorenz0]

Now on to $$I_{5m}=\frac{P}{4\pi R^2}$$This is for an isotropic source. But not for your laser!

I don't know the formula for the non-isotropic case so I thought I could modify that one and use as radius the one I got from the angular divergence.

 

[haruspex]

I am suspicious of these results since I never had to use the wavelength \lambda so I think my definition of angular divergence is wrong;

The item on Gaussian laser beams at https://en.m.wikipedia.org/wiki/Beam_divergence shows how the wavelength can be relevant, but since you are not given the aperture at source it does not seem relevant here.

 

[lorenz0]

The item on Gaussian laser beams at https://en.m.wikipedia.org/wiki/Beam_divergence shows how the wavelength can be relevant, but since you are not given the aperture at source it does not seem relevant here.

That is exactly what I thought too.

 

[haruspex]

Thanks, it should be correct now.

Doesn’t seem quite right. It has to illuminate an area $4\pi D^2$ instead of $\frac 14\pi(D\theta)^2$. So I get $3mW*\frac{16}{\theta^2}$, which is about 1.5MW.

 

[BvU]

@lorenz0 : you grasp this factor 4 now ?

Final note: when you get input of 1 or 2 digit accuracy, don't provide a result wih 6 digits.

$\$