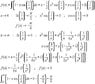- #1
Nebuchadnezza
- 79
- 2
This is not a bookquestion by far. It does have a nice solution, but I am stumpled on how to get it
[tex] \int_{0}^{\infty} 1 - x \, \sin \left( \frac{1}{x} \right) \, \text{dx} [/tex]
Now I could split the integrals into two pieces, where the first part obviously goes towards infinity. The second integral also seem to tend to infinity but at a slower pace, which makes the integral converge.
I tried to make a serie expansion of the sine, but that did not work out. The answer is supposed to be [tex]\frac{\pi}{4}[/tex]
Any hints, tips or solutions?
Another problem is that [tex] x \, \sin \left( \frac{1}{x} \right)[/tex] oscillates faster and faster when approaching zero. The limit is zero, but this confuses me...
[tex] \int_{0}^{\infty} 1 - x \, \sin \left( \frac{1}{x} \right) \, \text{dx} [/tex]
Now I could split the integrals into two pieces, where the first part obviously goes towards infinity. The second integral also seem to tend to infinity but at a slower pace, which makes the integral converge.
I tried to make a serie expansion of the sine, but that did not work out. The answer is supposed to be [tex]\frac{\pi}{4}[/tex]
Any hints, tips or solutions?
Another problem is that [tex] x \, \sin \left( \frac{1}{x} \right)[/tex] oscillates faster and faster when approaching zero. The limit is zero, but this confuses me...
Last edited: