Interference of 2 spherical waves

In summary, the conversation discusses finding the curvature C2 through ABCD matrices and mentions that C1 has only one phase inversion compared to C. The resulting pattern is similar to Newton's rings, but the sizes of the rings cannot be determined without knowing the lens parameters. The position of C1 and C2's centers are not given, but C1's radius of curvature is thought to be the sum of the distances from the planar surface to the point source and the center of C1.
  • #1
mariamiguel1921
1
0
Homework Statement
I have these image and I have difficulties in solving two questions.
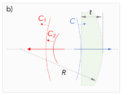
The first asks to write the curvature of the spherical waves, C1 and C2 after reflecting in the plane and spherical front respectively, as a function of R, radius of curvature of the lens, n index of refraction of the lens and t, the thickness of the lens.
And the second , which asks what the interference pattern is like if the two wavefronts with curvatures C1 and C2 interfere at
a distance −d from the flat face of the lens.
Relevant Equations
none
I believe that to find the curvature C2 is through the ABCD matrices and that C1 has only one phase inversion compared to C. In addition, that the pattern formed is like Newton's rings but I don't know how to find the sizes of the newton's rings depending on lens parameters
 

Attachments

  • Capturar.PNG
    Capturar.PNG
    5.7 KB · Views: 85
Physics news on Phys.org
  • #2
The way C is drawn, with that blue arrow angled up from the horizontal, it appears to be from a point source some distance to the left. If that point is ##x_1## from the planar surface and the centre of C1 is ##x_2## from the planar surface then I would have thought C1's radius of curvature was ##x_1+x_2##. But ##x_2## is not given.
Likewise, the position of the centre of C2 is not given.
 

FAQ: Interference of 2 spherical waves

What is interference of two spherical waves?

Interference of two spherical waves occurs when two waves originating from different points in space overlap and combine. The resulting wave pattern is a superposition of the two individual waves, leading to regions of constructive interference (where the waves reinforce each other) and destructive interference (where the waves cancel each other out).

How do the sources' distances affect the interference pattern?

The distances between the sources of the spherical waves significantly influence the interference pattern. If the sources are closer together, the interference fringes (regions of constructive and destructive interference) will be more widely spaced. Conversely, if the sources are farther apart, the fringes will be closer together. The spatial relationship between the sources and the observation point determines the specific pattern observed.

What role does wavelength play in the interference of spherical waves?

The wavelength of the spherical waves is crucial in determining the interference pattern. Shorter wavelengths result in more closely spaced interference fringes, while longer wavelengths produce fringes that are spaced further apart. The wavelength also affects the intensity and clarity of the interference pattern, with specific wavelengths leading to more pronounced constructive and destructive interference regions.

Can interference of spherical waves be observed in everyday life?

Yes, interference of spherical waves can be observed in everyday life, although it might not always be obvious. Examples include the patterns created by sound waves from multiple sources, the interference of light waves leading to colorful patterns on soap bubbles or oil films, and the overlapping ripples in water when two stones are thrown close to each other. These phenomena all demonstrate the principles of wave interference.

How can the interference pattern of two spherical waves be mathematically described?

The interference pattern of two spherical waves can be mathematically described using the principle of superposition. The resulting wave function is the sum of the individual wave functions from each source. For two spherical waves originating from points (x1, y1, z1) and (x2, y2, z2), the resultant wave at any point (x, y, z) can be expressed as the sum of the amplitudes and phases of the two waves, often involving complex exponential functions to account for phase differences and distances from the sources.

Similar threads

How Do Newton Rings Help Calculate Lens Curvature?
Replies
4
Views
3K
Circular Interference, Newton's Rings
Replies
11
Views
13K
Newton rings: spherical droplet with thin film interference
Replies
1
Views
2K
Determining Wave Parameters for Interference Pattern
Replies
3
Views
3K
Interference Maxima and Newton's Rings (Please help with trig)
Replies
4
Views
3K
Question about wave interference and coherence
Replies
8
Views
2K
Some multiple choice questions.
Replies
2
Views
1K
I Photon interference and beamforming
2
Replies
64
Views
4K
Archived Understanding Interference Patterns and the Wave/Particle Duality of Light
Replies
1
Views
2K
I 2-photon interference question
3
Replies
76
Views
5K

Hot Threads

Recent Insights

Back
Top