Physics Forums: Science Discussion, Homework Help, Articles
I want to split a fat laser beam and interfere it with itself, kind of like this:
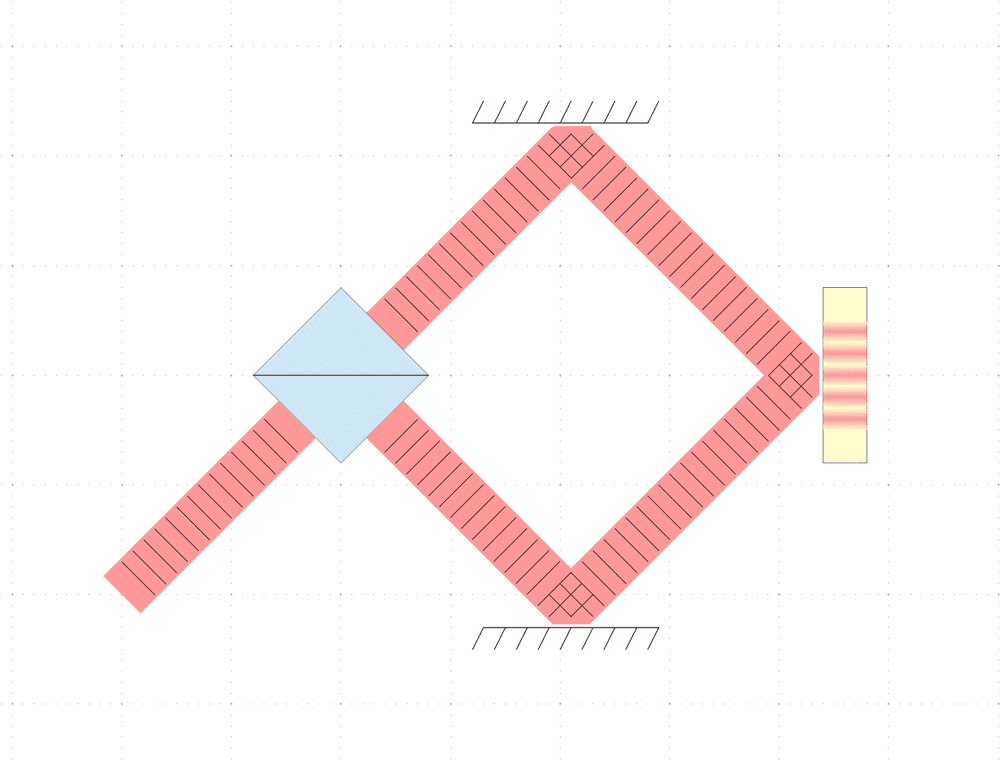
The very obvious problem is that the wave peaks shown as black lines would be a whole lot closer together, so the interference fringes would be sub-microscopic. If a couple of glass wedges - oddly-shaped prisms - were inserted into the two sub-beams, could that cause the wave peaks to be almost horizontal such that the interference fringes were visible? Something like this:
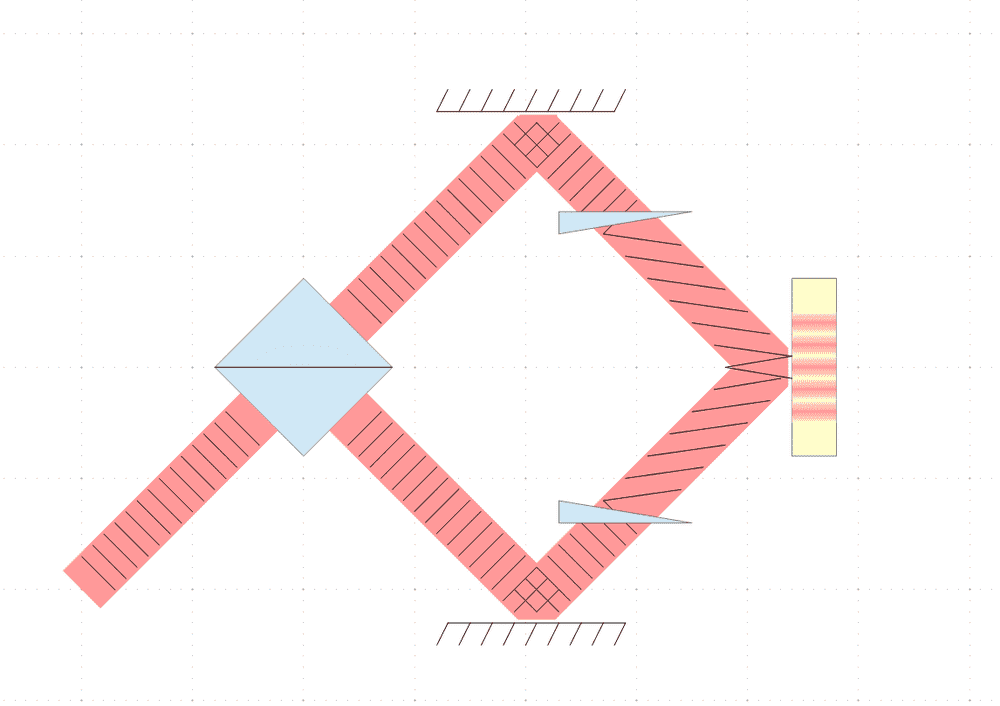
I don't know exactly how the waves behave in glass but can take a stab at it. I would think the entire wave would hit it's peak at the same time, and since the light is going through a medium with a refractive index greater than space or air, parts of the thick beam would be delayed more than others. It would vary linearly across the width of the beam. Tuning the orientation of the glass wedges to get exactly the right angle of the wave peaks would be difficult but not impossible.
A related question is about how to make a beam fat in the first place. Two lenses with different focal lengths can make a beam expnader, but what does that do to the wave peaks? When the beam comes out the second lens, would the waves all be perpendicular to the beam direction as they were before expansion, or would they be curved across its width? If the latter is the case, interfering them again would be painful.
I am talking about the probability density wave, not the electromagnetic wave.
If the wedge idea isn't possible, another idea would be to take, pentagonal prisms - not the right-angle pentaprisms used to reverse images - that are kind of a regular pentagon shape and insert the two sub-beams in two of the consecutive faces such that the come out almost parallel and almost on top of each other, then fully interfere after a short distance. That, of course, has its own problems, specifically in that I can't find such a prism and haven't done the math to make sure it would work - see above questions regarding how to do these calculations.
The very obvious problem is that the wave peaks shown as black lines would be a whole lot closer together, so the interference fringes would be sub-microscopic. If a couple of glass wedges - oddly-shaped prisms - were inserted into the two sub-beams, could that cause the wave peaks to be almost horizontal such that the interference fringes were visible? Something like this:
I don't know exactly how the waves behave in glass but can take a stab at it. I would think the entire wave would hit it's peak at the same time, and since the light is going through a medium with a refractive index greater than space or air, parts of the thick beam would be delayed more than others. It would vary linearly across the width of the beam. Tuning the orientation of the glass wedges to get exactly the right angle of the wave peaks would be difficult but not impossible.
A related question is about how to make a beam fat in the first place. Two lenses with different focal lengths can make a beam expnader, but what does that do to the wave peaks? When the beam comes out the second lens, would the waves all be perpendicular to the beam direction as they were before expansion, or would they be curved across its width? If the latter is the case, interfering them again would be painful.
I am talking about the probability density wave, not the electromagnetic wave.
If the wedge idea isn't possible, another idea would be to take, pentagonal prisms - not the right-angle pentaprisms used to reverse images - that are kind of a regular pentagon shape and insert the two sub-beams in two of the consecutive faces such that the come out almost parallel and almost on top of each other, then fully interfere after a short distance. That, of course, has its own problems, specifically in that I can't find such a prism and haven't done the math to make sure it would work - see above questions regarding how to do these calculations.