Intermediate Value Theorem .... Browder, Theorem 3.16 .... ....

[Math Amateur]

TL;DR Summary

I need help with an aspect of the proof of the Intermediate Value Theorem ...

I am reading Andrew Browder's book: "Mathematical Analysis: An Introduction" ... ...

I am currently reading Chapter 3: Continuous Functions on Intervals and am currently focused on Section 3.1 Limits and Continuity ... ...

I need some help in understanding the proof of Theorem 3.16 ...Theorem 3.16 and its proof read as follows:

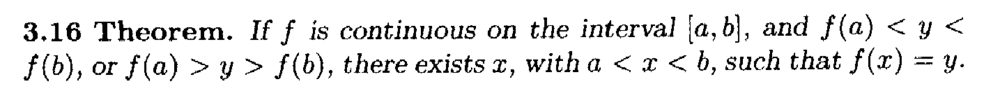
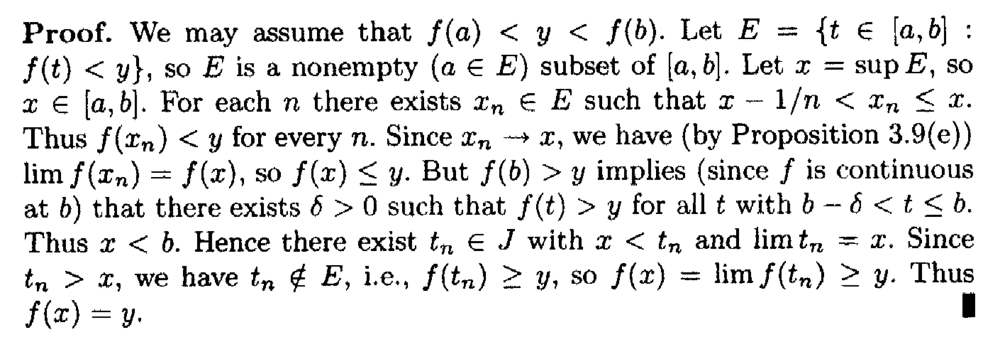
In the above proof by Andrew Browder we read the following:

" ... ... But $f(b) \gt y$ implies (since $f$ is continuous at $b$) that there exists $\delta \gt 0$ such that $f(t) \gt y$ for all $t$ with $b - \delta \lt t \leq b$. ... ... "My question is as follows:

How do we demonstrate explicitly and rigorously that since $f$ is continuous at $b$ and $f(b) \gt y$ therefore we have that there exists $\delta \gt 0$ such that $f(t) \gt y$ for all $t$ with $b - \delta \lt t \leq b$. ... ...Help will be much appreciated ...

Peter

***NOTE***

The relevant definition of one-sided continuity for the above is as follows:

$f$ is continuous from the left at $b$ implies that for every $\epsilon \gt 0$ there exists $\delta \gt 0$ such that for all $x \in [a, b]$ ...

we have that $b - \delta \lt x \lt b \Longrightarrow \mid f(x) - f(b) \mid \lt \epsilon$

 

[member 587159]

I hate proofs like these. They obscure what's really happening. General topology and the notions of connectedness and compactness immediately imply your theorem.

However, the question you ask is very straightforward to anwer.

Since $f(b)>y$, we have $\epsilon:= f(b)-y>0$. Now use the definition of continuity with this choice of $\epsilon$.

Draw a picture to see how I came up with this choice of $\epsilon$.

 

[Math Amateur]

I hate proofs like these. They obscure what's really happening. General topology and the notions of connectedness and compactness immediately imply your theorem.

However, the question you ask is very straightforward to anwer.

Since $f(b)>y$, we have $\epsilon:= f(b)-y>0$. Now use the definition of continuity with this choice of $\epsilon$.

Draw a picture to see how I came up with this choice of $\epsilon$.

Thank you for a most interesting and informative reply ...

Will now look at other proofs to see how concepts of compactness and connectedness imply theorem ...

Will also work on your suggestion ...

Thanks again,

Peter

 

[mathwonk]

It is of course easy to prove that the continuous image of a connected set is connected, but I think it is not so easy to prove an interval is connected without essentially the same argument using least upper bounds; indeed that fact is essentially equivalent to the intermediate value theorem. One of my favorite definitions of connectedness is that a set S is connected iff every continuous map S-->{0,1} is constant, where {0,1} is the two point set containing only 0 and 1. It is easy to show this special case is equivalent to the full intermediate value theorem. So I could be wrong but I am afraid you are stuck with some such proof using sups. i.e. least upper bounds.

 

[Math Amateur]

Thanks for a very interesting post, mathwonk ...

Indeed, having consulted several texts on the IVT I have found, as you predict, that the proof involves sups in each case ...

Thanks again ...

Peter