- #1
hdp12
- 68
- 2
I'm working on a homework problem for Statics and I'm stuck. Could someone please help?Problem: Draw the internal force (N,V,M) diagrams and include all significant figures
 Here is all of my work:
Here is all of my work:
W(x) = W1
∴ F2=∫02b W1dx
DIAGRAM:
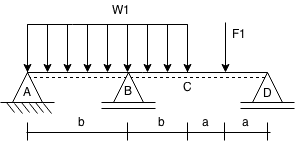
[+→]∑Fx = 0 : 0 = RAX
→RBY⋅b + RDY(2b+2a) = W1⋅2b⋅b + F1(2b + a)
SEPARATE FBDs:
[+CW]∑MB = 0 : 0 = RAY⋅b
So now, using eq's (8) & (9) in eq (4) we can determine RDY
eq (4) : RAY + RBY + RDY = F1 + W1⋅2b
→F2 + RDY = F1 + W1⋅2b
→ RDY = F1 + W1⋅2b - W1⋅2b
(9) > (5) : F2⋅b + RDY(2b+2a) = 2⋅W1⋅b2 + F1(2b + a)
→ RDY(2b+2a) = 2⋅W1⋅b2 + F1(2b + a) - (W1⋅2b)⋅b
→ RDY= 1/(2b+2a)[F1(2b + a) + 2⋅W1⋅b2 - (W1⋅2b)⋅b]
→ RDY= F1(2b + a)/(2b+2a)I'm just super lost, I guess, on where to go and if I'm even starting in the right direction... could someone please help me?
Resulting F from W1:
∴ F2=∫02b W1dx
eq (1) ⇒ F2 = W1⋅2b
x1 = (F1)-1 ∫02b W1dx = 1/(W1⋅2b)⋅(W1/2 ⋅ x2) |02b eq (2) ⇒ x1 = b;
SUPPORT REACTIONS DIAGRAM &FBD:
FBD:
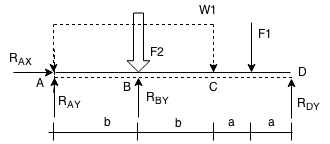
SUPPORT REACTIONS VARIABLE SOLUTION:
SUPPORT REACTIONS VARIABLE SOLUTION:
eq (3) ⇒ RAX = 0 ;
[+∧]∑Fy = 0 : 0 = (RAY + RBY + RDY) - (F1 + F2) eq (4) ⇒ RAY + RBY + RDY = F1 + W1⋅2b;
[+CW]∑MA = 0 : 0 = (F2⋅b + F1(2b + a)) - (RBY⋅b + RDY(2b+2a))→RBY⋅b + RDY(2b+2a) = W1⋅2b⋅b + F1(2b + a)
eq (5) ⇒ RBY⋅b + RDY(2b+2a) = 2⋅W1⋅b2 + F1(2b + a) ;
[+CW]∑MB = 0 : 0 = (RAY⋅b + F1(b+a)) - RDY(b+2a)eq (6) ⇒ RDY(b+2a) = RAY⋅b + F1(b+a) ;
[+CCW]∑MB = 0 : 0 = (F1⋅a + F2(2a+b)) - (RBY(2a+b)+RAY(2b+2a))eq (7) ⇒ RBY(2a+b)+RAY(2b+2a) = F1⋅a + F2(2a+b) ;
SEPARATE FBDs:
I:
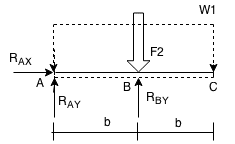 II:
II:
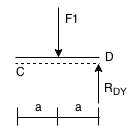
Separating the system at the hinge (C) will allow us to solve for the support reactions: In Figure 1, we can solve for the support reactions in the separate part, and therefore solve for the support reactions in the whole beam.
[+CW]∑MB = 0 : 0 = RAY⋅b
eq (8) ⇒ RAY = 0 ;
[+∧]ΣFy = 0 : 0 = RAY + RBY - F2eq (9) ⇒ RBY = F2
So now, using eq's (8) & (9) in eq (4) we can determine RDY
eq (4) : RAY + RBY + RDY = F1 + W1⋅2b
→F2 + RDY = F1 + W1⋅2b
→ RDY = F1 + W1⋅2b - W1⋅2b
eq (10) ⇒ RDY = F1
(9) > (5) : F2⋅b + RDY(2b+2a) = 2⋅W1⋅b2 + F1(2b + a)
→ RDY(2b+2a) = 2⋅W1⋅b2 + F1(2b + a) - (W1⋅2b)⋅b
→ RDY= 1/(2b+2a)[F1(2b + a) + 2⋅W1⋅b2 - (W1⋅2b)⋅b]
→ RDY= F1(2b + a)/(2b+2a)I'm just super lost, I guess, on where to go and if I'm even starting in the right direction... could someone please help me?