- #1
Sirsh
- 267
- 10
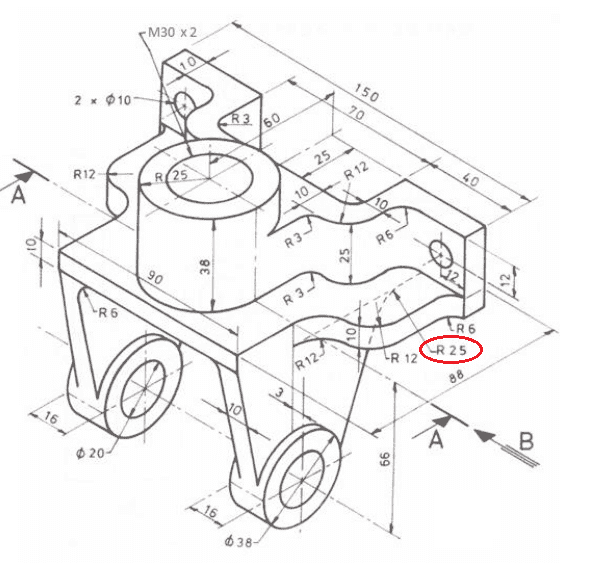
I am trying to create a third angle projection of this isometric drawing and for the most part it is very straight forward. However, I cannot figure out where to position a 'circle' of radius 25 to give me the correct curvature that is required for this drawing.
Whenever I locate a circle and then try to connect a straight line to it, I get some awkward connection as seen below where it seems like there is a 'jump'.
Here is the isometric drawing that I have (red is the dimension I'm having issues with):
Attempt 1:

Attempt 2:

Any help is much appreciated!
Whenever I locate a circle and then try to connect a straight line to it, I get some awkward connection as seen below where it seems like there is a 'jump'.
Here is the isometric drawing that I have (red is the dimension I'm having issues with):
Attempt 1:
Attempt 2:
Any help is much appreciated!