- #1
naushaan
- 20
- 2
- TL;DR Summary
- Hi guys, I'm having trouble with interpreting scale-factor and distance graphs of Type 1a supernovae.
'Imagine that you live in a different universe, which may have a different cosmology to our own. You measure the distances to and redshifts of a large number of Type Ia supernovae, and you use the redshifts to calculate the scale-factor of the universe at the time when the supernova exploded. You get the following graph of distances and scale-factors.'
The question is asking to deduce as much as you can from the plot below:
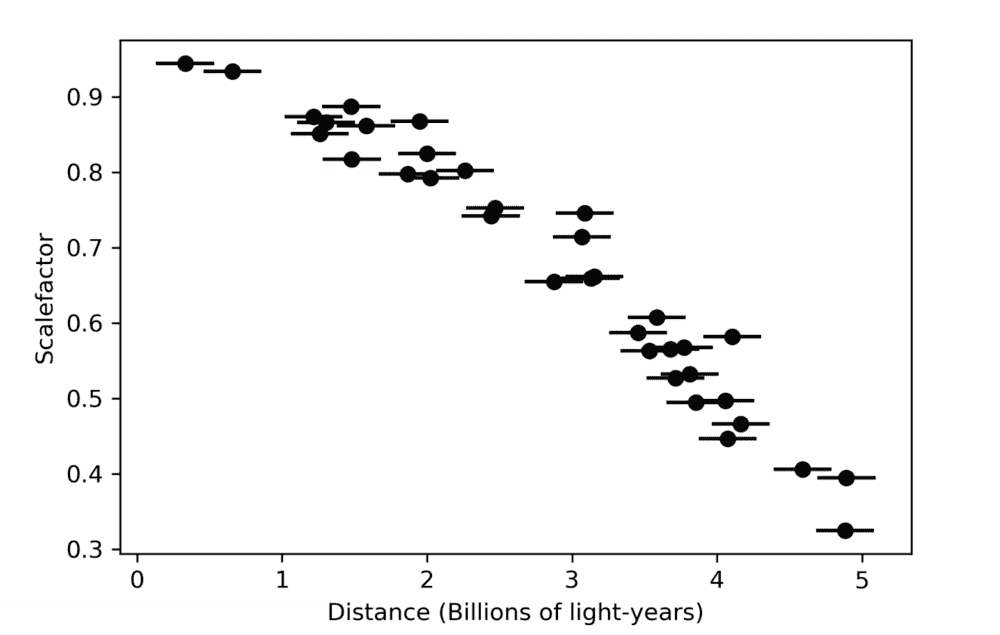
The question is asking to deduce as much as you can from the plot below: