Interpreting Weird Results: J_u, P_1 and T_1

[baseballfan_ny]

Homework Statement

A sheet (“sheet 1”) of area A having emissivity $e_1$ is held at temperature $T_1$ so that it emits a total power $P_1$ to the right (i.e., energy per unit time). Let σB be the Stefan-Boltzmann constant and neglect all edge effects.

a. In terms of $P_1$, calculate temperature $T_1$ of sheet 1.

Two additional black sheets, each of area A and having emissivities $e_2$ = 1 and $e_3$ = 1, are now added to the right of sheet 1. (See figure below) The spacings between the pairs of sheets is d, such that $d^2$ is much less than A . The temperature $T_2$ of the middle sheet (2) is allowed to vary and the right-hand sheet (3) is held at a fixed temperature $T_3$ = 0.

b. Assume that sheet 2 reaches a steady state temperature $T_2$. What is the power flow $P_{23}$ (total power, not power per unit area) emitted by sheet 2 to the right-hand sheet, i.e., from sheet 2 to sheet 3? Your answer should be given in terms of in terms of $T_2$, A, d, $\sigma_B$, and $e_1$ only. [Note: Not all of these parameters should appear in your answer.]

c. Determine $T_2$ in terms of $T_1$, A, d, $\sigma_B$ and $e_1$ only.

Relevant Equations

Stefan-Boltzmann
$J_u = e \sigma_B T^4$

I need someone to check my work, because I'm getting weird results that I'm not able to interpret physically for parts b and c. Thanks in advance.

For part a...

$J_u = e_1 \sigma_B T^4$
$P_1 = AJ_u = e_1 \sigma_B AT_1^4$
$T_1 = \left( \frac {P_1} {e_1 \sigma_B A} \right)^{\frac 1 4}$

For part b...

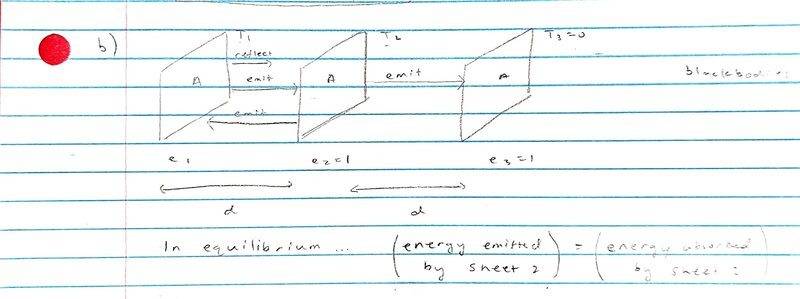
I'm using the idea that energy emitted by sheet 2 = energy absorbed by sheet 2

$\sigma_B T_2^4 + \frac {P_{23}} {A} = e_1 \sigma_B T_1^4 + (1 - e_1) \sigma_B T_2^4$
$\frac {P_{23}} {A} = e_1 \sigma_B \left( T_1^4 - T_2^4 \right)$
$P_{23} = A e_1 \sigma_B \left( T_1^4 - T_2^4 \right)$

For part c...

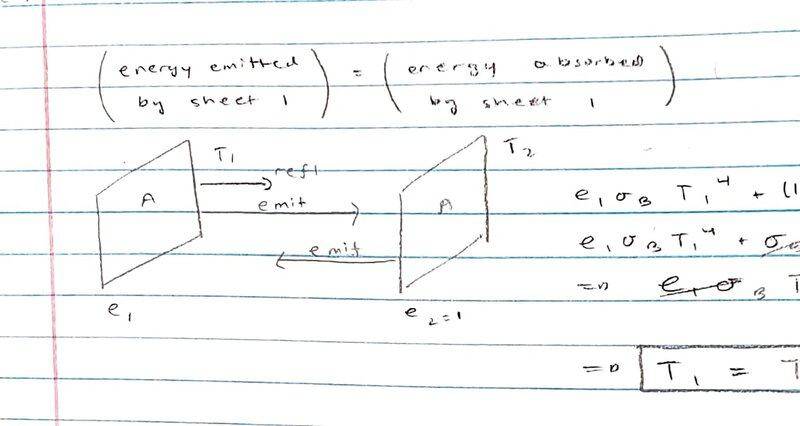
I'm using the idea that energy emitted by sheet 1 = energy absorbed by sheet 1

$e_1 \sigma_B T_1^4 + \left( 1 - e_1 \right) \sigma_B T_2^4 = \sigma_B T_2^4$
$e_1 \sigma_B T_1^4 = e_1 \sigma_B T_2^4$
$T_1 = T_2$

Now this has been bothering me, because if $T_1 = T_2$, then $P_{23} = 0$? I can't seem to make sense of that.

 

[haruspex]

For part b...
View attachment 291135
I'm using the idea that energy emitted by sheet 2 = energy absorbed by sheet 2

$\sigma_B T_2^4 + \frac {P_{23}} {A} = e_1 \sigma_B T_1^4 + (1 - e_1) \sigma_B T_2^4$

I don't see how you get this equation. Surely emissions from the third sheet are part of the middle sheet's energy balance. And can't you immediately write down how $P_{23}$ depends on $T_2$ without reference to the other sheets?

 

[baseballfan_ny]

Surely emissions from the third sheet are part of the middle sheet's energy balance.

But $T_3$ = 0, so it doesn't emit any energy, right? I suppose it can absorb energy emitted by $P_{23}$.

And can't you immediately write down how P23 depends on T2 without reference to the other sheets?

I had thought that originally ... that $P_{23} = A\sigma_B T_2^4$, but I think there has to be equilibrium maintained? So that's why applied those conditions.

I just don't think it makes sense for $P_{23} = 0$.

 

[haruspex]

But T3 = 0

Sorry, I missed that.

I had thought that originally ... that $P_{23} = A\sigma_B T_2^4$, but I think there has to be equilibrium maintained?

That equation is a valid answer whether or not equilibrium is maintained. The answer you gave includes T1, which is not allowed.

I'm using the idea that energy emitted by sheet 1 = energy absorbed by sheet 1

$e_1 \sigma_B T_1^4 + \left( 1 - e_1 \right) \sigma_B T_2^4 = \sigma_B T_2^4$

Please explain how you get that equation.
One thing I am not clear on is whether you are supposed to assume all arriving energy is absorbed, or whether in each case absorptivity equals emissivity, so (1-e) would be reflected (much complicating matters).

 

[baseballfan_ny]

Please explain how you get that equation.

My idea was that the total amount of energy emitted by sheet 1 = total amount of energy "delivered" to sheet 1 (I realized I wrote "absorbed" instead of "delivered" in Post 1 so that was probably confusing). The first term is the energy emitted by sheet 1, since it has absorptivity = emissivity = $e_1$. The 2nd term was the amount of energy (originating from sheet 2) reflected by sheet 1. The right hand side is the amount of energy delivered to sheet 1 from sheet 2.

One thing I am not clear on is whether you are supposed to assume all arriving energy is absorbed, or whether in each case absorptivity equals emissivity, so (1-e) would be reflected (much complicating matters).

I believe I'm supposed to take $a = e$ by Kirchoff's Law.

That equation is a valid answer whether or not equilibrium is maintained. The answer you gave includes T1, which is not allowed.

Ok so I'm getting something new. I think I'm supposed to say sheet 2 emits $J = \sigma_B T_2^4$ and then enforce equilibrium.

So then my answer to part b would just be...
$P_{23} = A \sigma_B T_2^4$.

Then for part c I would enforce equilibrium on sheet 2... that however much is absorbed by it is emitted...

$(1 - e_1)\sigma_B T_2^4 + e_1 \sigma_B T_1^4 = \sigma_B T_2^4$

where the first term is the amount reflected by sheet 1 and reabsorbed by sheet 2, the second term is the amount emitted by sheet 1 and absorbed by sheet 2, and the right hand side term is the amount emitted by sheet 2.

So...

$\sigma_B T_2^4 - e_1\sigma_B T_2^4 + e_1\sigma_B T_1^4 = \sigma_B T_2^4$

$- e_1\sigma_B T_2^4 + e_1\sigma_B T_1^4 = 0$

$T_1 = T_2$, but as you pointed out, $P_{23} = A \sigma_B T_2^4$ and should not be in terms of $T_1$ so I no longer have $P_{23} = 0$

 

[haruspex]

My idea was that the total amount of energy emitted by sheet 1 = total amount of energy "delivered" to sheet 1

You cannot assume the emissions and absorptions of sheet 1 are in balance. There will surely be a net flow of energy from 1 to 3, even though 2 is at a constant temperature.

The 2nd term was the amount of energy (originating from sheet 2) reflected by sheet 1

If you have to allow for reflections then there are in principle infinitely many.
Create unknowns for the total flow from 1 to 2 and 2 to 1 and write equations relating these to the emissions and absorptions.