PaulMuadDib
- 11
- 4
Hi there,
I am not a thermal sciences specialist, and I try go get an idea of the insulation required to retain heat in a sand battery for a few months.
I have a small pool (4 x 2 x 1.5 m) and I am questionning myself about two options: either converting this pool into a water storage or into a heat storage (heating sand during summer).
I have tried a very simple modelling (differential equation) to get an idea of the needed insulation for this interseasonal heat storage:
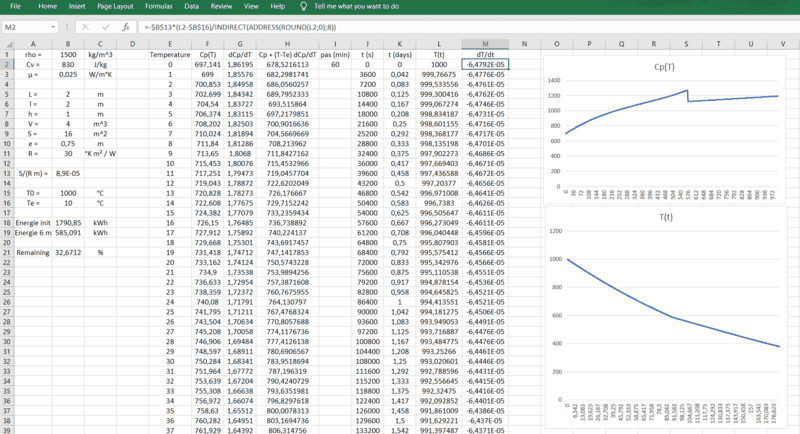
dQ/dt = m [ Cp + (T-Tex) dCp/dT ] dT/dt = - S phi = - S/R (T - Text)
where m is the mass (kg) of sand, Cp is the heat capacity (J/kg.°K) of sand (varying with temperature, capturing the quartz inversion), S is the surface of the sand volume (to be insulated), R is the thermal resistance (R value in °K.m²/W) of the insulator (I take one of the best: lambda = 0.025 °K.m²/W for polyurethane).
I am very surprised to see that I would need 75 cm thick polyuretane walls (R-value of 30 !) to get enough heat remaining after 6 months (meaning 400°C left or 35 % of the thermal energy left, starting from 1000°C), knowing these walls would not stand these high temps: is this realistic ? (for the R-value & the modelling) If not, how should I model this ?
I am not a thermal sciences specialist, and I try go get an idea of the insulation required to retain heat in a sand battery for a few months.
I have a small pool (4 x 2 x 1.5 m) and I am questionning myself about two options: either converting this pool into a water storage or into a heat storage (heating sand during summer).
I have tried a very simple modelling (differential equation) to get an idea of the needed insulation for this interseasonal heat storage:
dQ/dt = m [ Cp + (T-Tex) dCp/dT ] dT/dt = - S phi = - S/R (T - Text)
where m is the mass (kg) of sand, Cp is the heat capacity (J/kg.°K) of sand (varying with temperature, capturing the quartz inversion), S is the surface of the sand volume (to be insulated), R is the thermal resistance (R value in °K.m²/W) of the insulator (I take one of the best: lambda = 0.025 °K.m²/W for polyurethane).
I am very surprised to see that I would need 75 cm thick polyuretane walls (R-value of 30 !) to get enough heat remaining after 6 months (meaning 400°C left or 35 % of the thermal energy left, starting from 1000°C), knowing these walls would not stand these high temps: is this realistic ? (for the R-value & the modelling) If not, how should I model this ?
Attachments
Last edited: