LMHmedchem
- 20
- 0
Hello,
I believe that this is the correct forum for this post but please let me know if otherwise.
I have the following data in R4,
This data is roughly in the form of, though this is in R3,
View attachment 8272
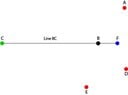
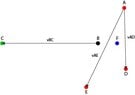
I need to find the coordinates for point F that is on line BC and also in the plane of A,D,E.
Generally, I guess that I would find the equation of the plane and the equation of the line and then the simultaneous solution for both equations. To find the equation of a plane, I would find the normal to the plane by taking the cross product of vectors AD and AE. Since the cross product is only defined in R3 and R7, I can't do this for R4, or any other dimensions.
I have vectors from point B to all other points and also vectors from point A to points D and E but I'm not sure how any of that helps. I assume that you can construct the equation for a hyperplane using a matrix operation, but I that's about as far as I have got with this.
I will code up the solution in c++ when I have a working method so I could use the Eigen library to to matrix operations if that is necessary.
Suggestions would be appreciated.
LMHmedchem
I believe that this is the correct forum for this post but please let me know if otherwise.
I have the following data in R4,
Code:
id x y z a
B -0.0700177 0.382249 -0.289338 0.00349957
A 1.13388 1.77602 -0.679365 -0.729256
D 3.97525 -0.0977321 -0.319119 0.864731
E -2.78909 0.10647 -0.206478 -0.0550962
C -35.0653177 -39.836051 23.355262 1.57447957This data is roughly in the form of, though this is in R3,
View attachment 8272
I need to find the coordinates for point F that is on line BC and also in the plane of A,D,E.
Generally, I guess that I would find the equation of the plane and the equation of the line and then the simultaneous solution for both equations. To find the equation of a plane, I would find the normal to the plane by taking the cross product of vectors AD and AE. Since the cross product is only defined in R3 and R7, I can't do this for R4, or any other dimensions.
I have vectors from point B to all other points and also vectors from point A to points D and E but I'm not sure how any of that helps. I assume that you can construct the equation for a hyperplane using a matrix operation, but I that's about as far as I have got with this.
I will code up the solution in c++ when I have a working method so I could use the Eigen library to to matrix operations if that is necessary.
Suggestions would be appreciated.
LMHmedchem