- #1
lordcx
- 3
- 0
intgration of a function*** help please***
actually this is not a homework, I found this explanation in a journal paper but I could not understand it. Can someone give me an explanation or possibly a proof that:
if:

then why integration over whole period is:
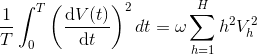
I have problem with the power of omega, my solution returns w with power 2, while the power of omega in answer is one, Can someone help me for the reason?
actually this is not a homework, I found this explanation in a journal paper but I could not understand it. Can someone give me an explanation or possibly a proof that:
Homework Statement
if:
then why integration over whole period is:
Homework Equations
I have problem with the power of omega, my solution returns w with power 2, while the power of omega in answer is one, Can someone help me for the reason?
Last edited:
