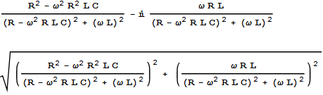SumDood_
- 39
- 6
- Homework Statement
- I am getting the wrong answer for Part B.
I don't understand if what I am doing for part C is correct.
- Relevant Equations
- Voltage divider rule
##V_{S} = 120V ##
##f = 60Hz##
##L = 20mH##
##R = 10\Omega ##
(a) Assume the capacitance is omitted. What is the resistor voltage?
##X_{L} = j\omega L = j2.4\pi##
##V_{R} = Vs\cdot \frac{R}{R+X_{L}} = 76.5067-j57.6847##
##V_{L} = Vs\cdot \frac{X_{L}}{R+X_{L}} = 43.493+j57.6847##
(b) What value of capacitance is required to make the resistor voltage have the same magnitude as the source voltage?
$$V_{R} = Vs\cdot \frac{R//X_{C}}{R//X_{C}+X_{L}}$$
$$R//C = \frac{R\cdot X_{C}}{R+X_{C}} = \frac{R\cdot \frac{1}{j\omega C}}{R+\frac{1}{j\omega C}} = \frac{R}{j\omega RC + 1}$$
$$V_{R} = Vs\cdot \frac{\frac{R}{j\omega RC + 1}}{\frac{R}{j\omega RC + 1}+j\omega L} = Vs\cdot \frac{R}{R+(j\omega L)(j\omega RC+1)}$$
$$V_{S} = V_{R} \equiv \frac{V_{R}}{V_{S}} = 1$$
$$1= \frac{R}{R+(j\omega L)(j\omega RC+1)}$$
$$(j\omega L)(j\omega RC+1) = 0$$
$$j\omega RC+1 = 0$$
$$C = \frac{-1}{j\omega R} = \frac{1}{120\pi\cdot 10} = 265.258\mu F$$
(c) What value of capacitance maximizes the resistor voltage? What is that maximum voltage?
$$V_{O} = V_{R} = Vs\cdot \frac{R}{R+(j\omega L)(j\omega RC+1)}$$
To increase the output voltage, I need to reduce the value of the denominator. I can do this by ##(j\omega RC+1) = 0## but this brings me back to the previous part of the question, which is incorrect for me.