FranzDiCoccio
- 350
- 43
- Homework Statement
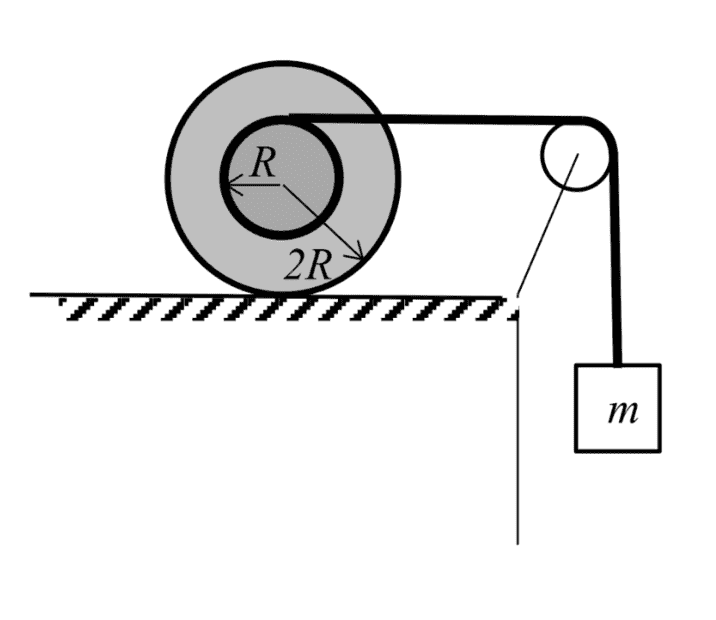
- an object is suspended by a rope that goes around a pulley and connects to a disc that is free to roll without sliding on a horizontal plane. The rope is coiled around a smaller disc welded onto the larger disc. Find the acceleration of the suspended object and the static friction between the plane and the disc.
- Relevant Equations
- second law of dynamics OR energy conservation plus uniformly accelerated motion
The figure illustrates the situation. The radii of the larger and smaller discs are 2R and R, respectively. Their masses are M and 2M, respectively (the largst disc has the smallest mass).
Also, m=5/4 M, where m is the mass of the suspended object. The pulley is "massless" (negligible moment of inertia).
One way of doing this is by writing three equations from the second law of dynamics: one for the acceleration of the object, one for the translational acceleration of the wheel, one for the rotational acceleration of the wheel. This is a system of three equations with three unknowns: the tension ##T## of the rope, the magnitude (and direction!) of the friction and the acceleration of the suspended object. These unknowns can be calculated.
A different approach consists in using energy conservation to find a relation between the translation of the object and its velocity. We expect this to be a uniformly accelerated motion, so we can calculate the acceleration.
In both cases I get
a = \frac{3}{7} g, \qquad F = \frac{1}{3} M g \qquad T = \frac{5}{7} Mg
I find there are two "tricky" points in this problem, which I hope I got right.
First, one has to realize that the acceleration of the object is ##a=3 R \alpha##.
This is because the wheel moves while the coil unwinds. So the displacement of the object is given by the displacement of the wheel plus the extra length of rope due to its unwinding.
The second tricky point is the direction of the friction. At first I naively thought it was opposite to the tension of the rope (i.e. leftwards).
However the equations suggest that friction goes from left to right. This makes sense, because the tension alone would generate an angular acceleration that is greater than ##\frac{a}{3R}##. The only "solution" is that friction cannot "add" to the torque of the tension, but has to hinder it.
It's kind of like when a car accelerates so much that its wheels slide on the street (bear with my English, I cannot find a better way of saying this).
And here comes my question: is there an intuitive argument for getting the direction of the friction right before solving the equations?
As I mention, when I first tried solving the problem I had to draw all the forces in order to write the second law for each object.
Since I originally chose the wrong direction for the friction, I obtained a "negative magnitude" for the friction.
This is not a big deal. It simply means I am working with the cartesian components of the forces, rather than with their magnitudes.
Still, I'm curious about an intuitive argument for the direction of the friction, which would allow one to work with magnitudes alone.
Thanks
Francesco
Also, m=5/4 M, where m is the mass of the suspended object. The pulley is "massless" (negligible moment of inertia).
One way of doing this is by writing three equations from the second law of dynamics: one for the acceleration of the object, one for the translational acceleration of the wheel, one for the rotational acceleration of the wheel. This is a system of three equations with three unknowns: the tension ##T## of the rope, the magnitude (and direction!) of the friction and the acceleration of the suspended object. These unknowns can be calculated.
A different approach consists in using energy conservation to find a relation between the translation of the object and its velocity. We expect this to be a uniformly accelerated motion, so we can calculate the acceleration.
In both cases I get
a = \frac{3}{7} g, \qquad F = \frac{1}{3} M g \qquad T = \frac{5}{7} Mg
I find there are two "tricky" points in this problem, which I hope I got right.
First, one has to realize that the acceleration of the object is ##a=3 R \alpha##.
This is because the wheel moves while the coil unwinds. So the displacement of the object is given by the displacement of the wheel plus the extra length of rope due to its unwinding.
The second tricky point is the direction of the friction. At first I naively thought it was opposite to the tension of the rope (i.e. leftwards).
However the equations suggest that friction goes from left to right. This makes sense, because the tension alone would generate an angular acceleration that is greater than ##\frac{a}{3R}##. The only "solution" is that friction cannot "add" to the torque of the tension, but has to hinder it.
It's kind of like when a car accelerates so much that its wheels slide on the street (bear with my English, I cannot find a better way of saying this).
And here comes my question: is there an intuitive argument for getting the direction of the friction right before solving the equations?
As I mention, when I first tried solving the problem I had to draw all the forces in order to write the second law for each object.
Since I originally chose the wrong direction for the friction, I obtained a "negative magnitude" for the friction.
This is not a big deal. It simply means I am working with the cartesian components of the forces, rather than with their magnitudes.
Still, I'm curious about an intuitive argument for the direction of the friction, which would allow one to work with magnitudes alone.
Thanks
Francesco