- #1
yuiop
- 3,962
- 20
There are various explanations for Thomas precession in the literature and I would like to come to a deeper understanding of the cause for this precession, so that maybe I can understand better whether Thomas rotation is applicable to the precession of a gyroscope orbiting around a gravitational body.
This paper gives an explanation in terms of an aircraft following a circular path. The argument is that if the circle is approximated by a polygon, then the angle for each corner of the polygon as measured by an observer on the aircraft is larger than the angle measured by an observer at rest with the polygon. One problem with this explanation is that it implies the rate of precession of the rod is constant (for constant angular velocity of the aircraft). This is not necessarily the case (See below). Another question is why should a gyroscope behave as if it is measuring angles of a path that is at rest in another reference frame?
The paper then converts the equation for the Thomas precession into a form that suggests that the precession is a result of centrifugal force. The problem with this interpretation is that an gyroscope in a perfect geodesic orbit around a gravitational body, experiences no proper forces, so no Thomas precession should occur. Then again, some authors would argue that Thomas precession does not occur in the gravitational orbit and this interpretation would support that view. To quote Wikipedia:
Another point of view is that Thomas precession is simply the result of the rotation that occurs when two consecutive non parallel Lorentz boosts are carried out. This is the interpretation outlined in this mathpages article. A consequence of this interpretation is that the precession rate for a given gyroscope is not constant for a constant velocity orbit. The diagram below illustrates this effect.
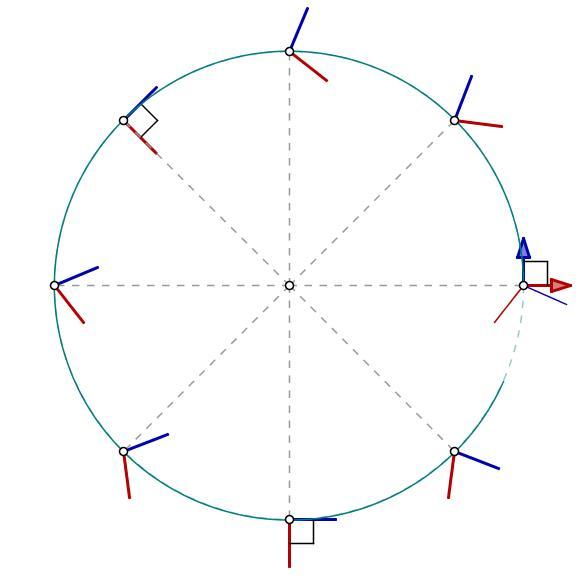
In the diagram two orthogonal gyroscopes (initially represented by the blue and red vectors) start at the 3 O'clock position and progress around the circle in an anticlockwise fashion. It can be seen that from the point of view of an inertial observer at rest with the centre of the circle, that the blue and red gyroscopes do not remain at right angles with respect to each other and do not precess by the same amount per complete 'orbit' unless by chance the angular velocity has certain critical values. The equation normally given for Thomas precession is just an average figure for many orbits. (Mathpages explains this in quite a lot of detail).
Finally page 235 of this paper by Malament gives a intuitive description of the precession of gyroscope being the result of the gyroscope following a path that deviates from the path of a photon that initially travels in the same direction. This has the nice quality that it applies in both Special and General relativity.
Which, if any, of the above explanations best describe what is really happening in Thomas precession?
P.S. Is aberration a factor? If an observer traveling in a circle points a telescope at a distant star and compares the direction the telescope is pointing relative to a gyroscope, will the angle of the telescope oscillate due to the periodically changing aberration factor, according to an inertial observer at the centre of the circle?
This paper gives an explanation in terms of an aircraft following a circular path. The argument is that if the circle is approximated by a polygon, then the angle for each corner of the polygon as measured by an observer on the aircraft is larger than the angle measured by an observer at rest with the polygon. One problem with this explanation is that it implies the rate of precession of the rod is constant (for constant angular velocity of the aircraft). This is not necessarily the case (See below). Another question is why should a gyroscope behave as if it is measuring angles of a path that is at rest in another reference frame?
The paper then converts the equation for the Thomas precession into a form that suggests that the precession is a result of centrifugal force. The problem with this interpretation is that an gyroscope in a perfect geodesic orbit around a gravitational body, experiences no proper forces, so no Thomas precession should occur. Then again, some authors would argue that Thomas precession does not occur in the gravitational orbit and this interpretation would support that view. To quote Wikipedia:
One can attempt to break down the de Sitter precession into a kinematic effect called Thomas precession combined with a geometric effect caused by gravitationally curved spacetime. At least one author[6] does describe it this way, but others state that "The Thomas precession comes into play for a gyroscope on the surface of the Earth ..., but not for a gyroscope in a freely moving satellite."[7] An objection to the former interpretation is that the Thomas precession required has the wrong sign.
Another point of view is that Thomas precession is simply the result of the rotation that occurs when two consecutive non parallel Lorentz boosts are carried out. This is the interpretation outlined in this mathpages article. A consequence of this interpretation is that the precession rate for a given gyroscope is not constant for a constant velocity orbit. The diagram below illustrates this effect.
In the diagram two orthogonal gyroscopes (initially represented by the blue and red vectors) start at the 3 O'clock position and progress around the circle in an anticlockwise fashion. It can be seen that from the point of view of an inertial observer at rest with the centre of the circle, that the blue and red gyroscopes do not remain at right angles with respect to each other and do not precess by the same amount per complete 'orbit' unless by chance the angular velocity has certain critical values. The equation normally given for Thomas precession is just an average figure for many orbits. (Mathpages explains this in quite a lot of detail).
Finally page 235 of this paper by Malament gives a intuitive description of the precession of gyroscope being the result of the gyroscope following a path that deviates from the path of a photon that initially travels in the same direction. This has the nice quality that it applies in both Special and General relativity.
Which, if any, of the above explanations best describe what is really happening in Thomas precession?
P.S. Is aberration a factor? If an observer traveling in a circle points a telescope at a distant star and compares the direction the telescope is pointing relative to a gyroscope, will the angle of the telescope oscillate due to the periodically changing aberration factor, according to an inertial observer at the centre of the circle?
Attachments
Last edited: