- #1
sophiatev
- 39
- 5
- TL;DR Summary
- I have questions about whether or not differential line elements for different geometries represent the same physical quantity, and about the Polar coordinate form of a differential line element in 2D Euclidean space.
In Hartle's book Gravity: An Introduction to Einstein's General Relativity he spends chapter 2 discussing some basic aspects of differential geometry. For example, he derives the expression for a differential line element in 2D Euclidean space:
dS^2 = (dx)^2 + (dy)^2 in Cartesian coordinates
dS^2 = (dr)^2 + (rdΦ)^2 in Polar coordinates
and also for a differential line element on the surface of a two-dimensional sphere of radius a:
dS^2 = a^2((dθ)^2 + sin^2(θ)(dΦ)^2)
My first question is, do these two line elements (for the plane and for the two-sphere) have the same physical length? Is the distance between two infinitely close points on the surface of any shape (sphere, egg, peanut) the same? Is this because at infinitesimal distances, curvature is non-existent?
My second question is it looks like the length of the line element for a plane, when expressed in polar coordinates, should increase at higher values of r. However, Hartle asserts that dS is a physically invariant quantity. Why does it not increase? Does it have something to do with the nature of multiplying by a differential, meaning that rdΦ is the same regardless of the value of r?
My third question is why a line element of the form
dS^2 = (dr)^2 + ((r + dr)dΦ)^2
is invalid. It seems to me that in this diagram he includes (forgive how faint the lines are)
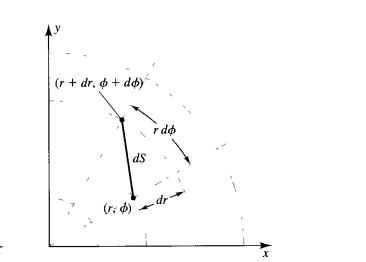
The rdΦ is closer to the (r + dr)dΦ arc length anyway. Furthermore, since (r + dr) is slightly bigger, (r + dr)dΦ seems closer to a straight line than rdΦ . Does this again have something to do with the fact that at infinitesimal lengths, both are considered completely straight? Either way, I don't see why my formulation would be invalid. It clearly is because if we convert from Cartesian to polar coordinates, starting with the Cartesian form of dS, we end up with Hartle's form of dS in polar coordinates. But I don't see why my expression for dS in polar coordinates is wrong just based on the diagram he provides.
dS^2 = (dx)^2 + (dy)^2 in Cartesian coordinates
dS^2 = (dr)^2 + (rdΦ)^2 in Polar coordinates
and also for a differential line element on the surface of a two-dimensional sphere of radius a:
dS^2 = a^2((dθ)^2 + sin^2(θ)(dΦ)^2)
My first question is, do these two line elements (for the plane and for the two-sphere) have the same physical length? Is the distance between two infinitely close points on the surface of any shape (sphere, egg, peanut) the same? Is this because at infinitesimal distances, curvature is non-existent?
My second question is it looks like the length of the line element for a plane, when expressed in polar coordinates, should increase at higher values of r. However, Hartle asserts that dS is a physically invariant quantity. Why does it not increase? Does it have something to do with the nature of multiplying by a differential, meaning that rdΦ is the same regardless of the value of r?
My third question is why a line element of the form
dS^2 = (dr)^2 + ((r + dr)dΦ)^2
is invalid. It seems to me that in this diagram he includes (forgive how faint the lines are)
The rdΦ is closer to the (r + dr)dΦ arc length anyway. Furthermore, since (r + dr) is slightly bigger, (r + dr)dΦ seems closer to a straight line than rdΦ . Does this again have something to do with the fact that at infinitesimal lengths, both are considered completely straight? Either way, I don't see why my formulation would be invalid. It clearly is because if we convert from Cartesian to polar coordinates, starting with the Cartesian form of dS, we end up with Hartle's form of dS in polar coordinates. But I don't see why my expression for dS in polar coordinates is wrong just based on the diagram he provides.