- #1
MarkFL
Gold Member
MHB
- 13,288
- 12
Here is the question:
Here is a link to the question:
A math function question please help? - Yahoo! Answers
I have posted a link there to this topic so that the OP may find my response.
A math function question please help?
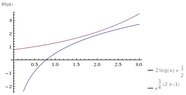
F(x) = a loge(x) + 1/2
Find the inverse which I found is e^x/a
It then said let a=2 and sketch graph which I did.
I'm getting trouble at this part
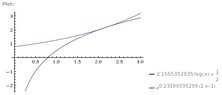
Find the value of a in 3 decimal places such that the graphs of y=f(x) and its inverse touch each other once only.
And hence find the contact point.
Please help explanations too please
Here is a link to the question:
A math function question please help? - Yahoo! Answers
I have posted a link there to this topic so that the OP may find my response.