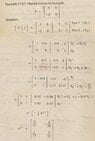zuby
- 4
- 0
Hi,
Can anyone help me to inverse the below matrix by row reduction method.
I know determinant method but I don't know row reduction method please help me.
4 5
-2 6
thanks.
Can anyone help me to inverse the below matrix by row reduction method.
I know determinant method but I don't know row reduction method please help me.
4 5
-2 6
thanks.