Investigating A Limit Via Graph

  • Thread starter Thread starter nycmathguy
  • Start date Start date
  • Tags Tags
    Graph Limit
nycmathguy
Homework Statement
Graphs and Limits
Relevant Equations
Quadratic and Piecewise Function
Use the graph to investigate

(a) lim of f(x) as x→2 from the left side.

(b) lim of f(x) as x→2 from the right side.

(c) lim of f(x) as x→2.

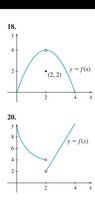
Question 18

For part (a), as I travel along on the x-axis coming from the left, the graph reaches a height of 4. The limit is 4. It does not matter if there is a hole at (2, 4), right?

For part (b), as I travel along on the x-axis coming from the right, the graph reaches a height of 4. The limit is 4. It does not matter if there is a hole at (2, 4), right?

For part (c), as I travel along on the x-axis coming from the left and right simultaneously, the graph reaches a height of 4. The limit is 4. It does not matter if there is a hole at (2, 4), right?

I conclude that the limit is 4.

You say?

I will answer 20 on a separate thread.
 

Attachments

  • Screenshot_20210613-160046_Drive.jpg
    Screenshot_20210613-160046_Drive.jpg
    9.6 KB · Views: 135
Physics news on Phys.org
nycmathguy said:
Question 18

For part (a), as I travel along on the x-axis coming from the left, the graph reaches a height of 4. The limit is 4. It does not matter if there is a hole at (2, 4), right?
Correct. The left-side limit if 4, and the presence of a hole doesn't matter.
nycmathguy said:
For part (b), as I travel along on the x-axis coming from the right, the graph reaches a height of 4. The limit is 4. It does not matter if there is a hole at (2, 4), right?
Correct. The right-side limit if 4, and the presence of a hole doesn't matter.
nycmathguy said:
For part (c), as I travel along on the x-axis coming from the left and right simultaneously, the graph reaches a height of 4. The limit is 4. It does not matter if there is a hole at (2, 4), right?

I conclude that the limit is 4.
Yes, correct.
 
Mark44 said:
Correct. The left-side limit if 4, and the presence of a hole doesn't matter.
Correct. The right-side limit if 4, and the presence of a hole doesn't matter.
Yes, correct.

I finally get one right on my own.
 

Thread 'Prove that the integral is equal to ##\pi^2/8##'

Prove $$\int\limits_0^{\sqrt2/4}\frac{1}{\sqrt{x-x^2}}\arcsin\sqrt{\frac{(x-1)\left(x-1+x\sqrt{9-16x}\right)}{1-2x}} \, \mathrm dx = \frac{\pi^2}{8}.$$ Let $$I = \int\limits_0^{\sqrt 2 / 4}\frac{1}{\sqrt{x-x^2}}\arcsin\sqrt{\frac{(x-1)\left(x-1+x\sqrt{9-16x}\right)}{1-2x}} \, \mathrm dx. \tag{1}$$ The representation integral of ##\arcsin## is $$\arcsin u = \int\limits_{0}^{1} \frac{\mathrm dt}{\sqrt{1-t^2}}, \qquad 0 \leqslant u \leqslant 1.$$ Plugging identity above into ##(1)## with ##u...
View full post »

Thread 'Finding the nth roots of a complex number'

There are two things I don't understand about this problem. First, when finding the nth root of a number, there should in theory be n solutions. However, the formula produces n+1 roots. Here is how. The first root is simply ##\left(r\right)^{\left(\frac{1}{n}\right)}##. Then you multiply this first root by n additional expressions given by the formula, as you go through k=0,1,...n-1. So you end up with n+1 roots, which cannot be correct. Let me illustrate what I mean. For this...
View full post »

Similar threads

Investigating Limit of Piecewise Function
Replies
2
Views
1K
Use Graph To Investigate Limit
Replies
7
Views
1K
Use the graph of f(x) to investigate the limit
Replies
6
Views
1K
Use Graph to Determine Limit: Calculating Limits with Piecewise Functions
Replies
3
Views
1K
Use Graph To Investigate Limit
Replies
10
Views
973
Use Graph To Investigate Limit
Replies
6
Views
1K
What Happens to f(x) as x Approaches 2?
Replies
15
Views
1K
Investigating Limits: What Happens When x Approaches a Constant or Zero?
Replies
1
Views
984
Investigate Limit of Piecewise Function
Replies
11
Views
1K
How Do Limits Behave for Piecewise Functions at Specific Points?
Replies
30
Views
2K

Hot Threads

Recent Insights

Back
Top