Noki Lee
- 4
- 1
Can we apply the 1d equation (dE/dx = labmda/epsilon0)dEdx=λϵ0 to the first and the second figures?
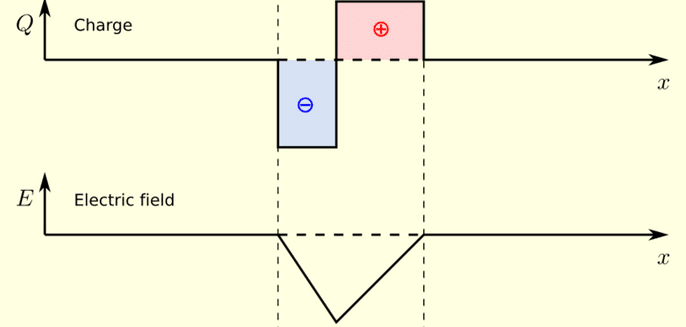
But, in the 2nd case,
if we integrate the charge density, some field exists between the two charge densities. Intuitively, it should be like the last figure.
What's wrong with this?
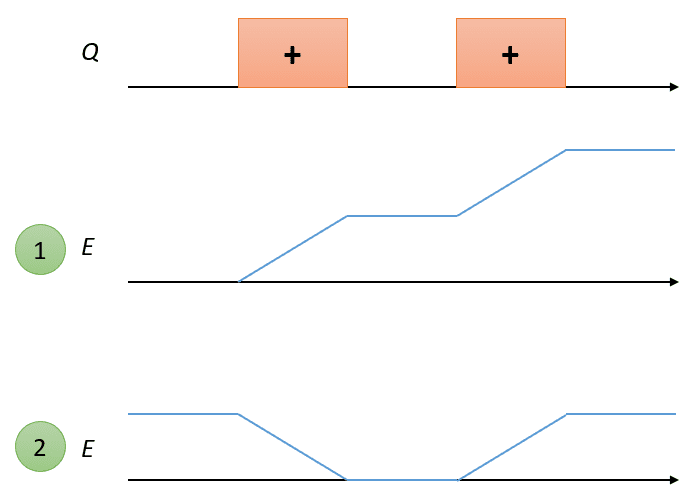
But, in the 2nd case,
if we integrate the charge density, some field exists between the two charge densities. Intuitively, it should be like the last figure.
What's wrong with this?