MHB Involute of a Circle and Grazing Area

[Chris L T521]

Thanks again to those who participated in last week's POTW! Here's this week's problem!

-----

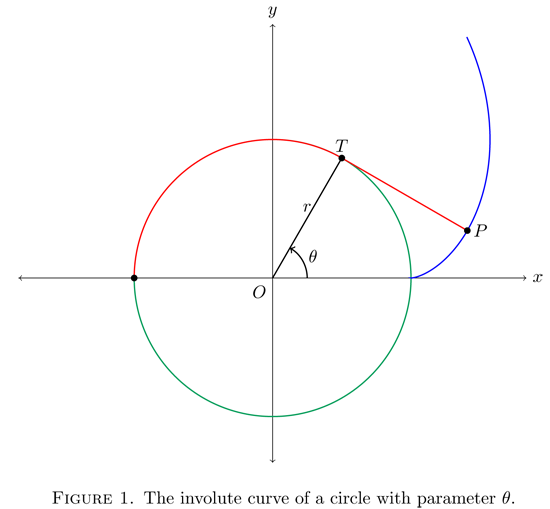
Background Info: A string is wound around a circle and then unwound while being held taut. The curve traced by the point $P$ at the end of the string is called the involute of the circle. If the circle has radius $r$ and center $O$ and the initial position of $P$ is $(r,0)$, and if the parameter $\theta$ is chosen as seen in Figure 1, then the parametric equations for the involute of the circle are
\[\left\{\begin{aligned} x(\theta) &= r \left(\cos\theta +\theta\sin\theta\right) \\ y(\theta) &= r\left(\sin\theta - \theta\cos\theta\right)\end{aligned}\right.\]

​

Problem: A cow is tied to a silo with radius $r$ by a rope just long enough to reach the opposite side of the silo. Find the area available for grazing by the cow.

-----

 

[Chris L T521]

This week's question was correctly answered by Deveno (welcome back, btw), MarkFL and Opalg. Since I liked each of their solutions, I'm going to post them all below.

Deveno's solution:

Spoiler

We can express the involute as a function of [math]\theta[/math] like so:

[math]f(\theta) = \sqrt{[x(\theta)]^2 + [y(\theta)]^2} = \sqrt{r^2(\cos\theta + \theta\sin\theta) + r^2(\sin\theta - \theta\cos\theta)}[/math]

[math]= r\sqrt{\cos^2\theta + 2\theta\cos\theta\sin\theta + \theta^2\sin^2\theta + \sin^2\theta - 2\theta\sin\theta\cos\theta + \theta^2\cos^2\theta}[/math]

[math]= r\sqrt{\cos^2\theta + \sin^2\theta + \theta^2(\cos^2\theta + \sin^2\theta)} = r\sqrt{1 + \theta^2}[/math].

Using polar integration, we find the area swept out by the involute above the x-axis as [math]\theta[/math] goes from [math]0[/math] to [math]\pi[/math] is:

[math]\frac{1}{2}\int_0^{\pi}\ (f(\theta))^2 d\theta = \frac{1}{2}\int_0^{\pi} r^2(1 + \theta^2) = \frac{1}{2}\left(\pi r^2 + \frac{\pi^3r^2}{3}\right)[/math].

By the symmetry of the problem, we can double this area, to eliminate the factor of 1/2.

At this point, the rope is taut tangent to the silo. On this "free side" of the silo, the cow can graze freely within a semi-circle of radius equal to the length of the rope, which is precisely half the *circumference* of the silo, that is: [math]\pi r[/math]. This adds the area of the semi-circle, which is, of course:

[math]\frac{1}{2}\pi(\pi r)^2 = \frac{\pi^3r^2}{2}[/math].

So, so far, we have an area of:

[math]\pi r^2 + \frac{\pi^3r^2}{3} + \frac{\pi^3r^2}{2} = \pi r^2 + \frac{5\pi^3r^2}{6}[/math].

Assuming the silo door is closed, and the cow cannot enter it, we must subtract the area of the silo itself (it probably has no grass in it anyway), leaving a total grazing area of:

[math]\pi r^2 + \frac{5\pi^3r^2}{6} - \pi r^2 = \frac{5\pi^3r^2}{6}[/math].

MarkFL's solution:

Spoiler

To avoid confusion, let's let the radius of the silo be 1 unit in length. After finding the area, we may then affix $r^2$ as a two-dimensional scaling factor. For now, we will use $r$ in our polar coordinate system.

There will be two portions of the area in which the cow can graze. The following diagram shows the "top" half as the area is symmetrical about the horizontal axis.

The light green area is the area between the involute and the silo, while the dark green area is where the rope is free from the silo except where it is attached and it is a quarter circle of radius $\pi$.

To find the area $A_1$ under the involute, we may use:

$$A_1=\frac{1}{2}\int_0^{\pi}r^2\,d\theta$$

where:

$$r^2=x^2+y^2=\left(\cos(\theta)+\theta\sin(\theta) \right)^2+\left(\sin(\theta)-\theta\cos(\theta) \right)^2$$

$$r^2=\cos^2(\theta)+2\theta\sin(\theta)\cos(\theta)+ \theta^2\sin^2(\theta)+\sin^2(\theta)-2\theta\sin(\theta)\cos(\theta)+ \theta^2\cos^2(\theta)$$

$$r^2=1+\theta^2$$

and so we have:

$$A_1=\frac{1}{2}\int_0^{\pi}1+\theta^2\,d\theta= \frac{1}{2}\left[\theta+\frac{1}{3}\theta^3 \right]_0^{\pi}=\frac{1}{2}\pi+\frac{1}{6}\pi^3$$

Subtracting the area of the silo in red (a semicircle of radius 1), we obtain:

$$A_1=\frac{1}{6}\pi^3$$

Next, the area in dark green is:

$$A_2=\frac{1}{4}\pi\cdot\pi^2=\frac{1}{4}\pi^3$$

And so, the total area $A$ available for grazing by the cow is (remembering to double and affix the scaling factor):

$$A=2r^2\left(A_1+A_2 \right)=2r^2\left(\frac{1}{6}\pi^3+\frac{1}{4}\pi^3 \right)=2r^2\left(\frac{5}{12}\pi^3 \right)=\frac{5}{6}\pi^3r^2$$

Opalg's solution:

Spoiler

First, note that the distance from the origin to the point $\bigl(r(\cos\theta + \theta\sin\theta), r(\sin\theta - \theta\sin\theta)\bigr)$ on the involute is $$\sqrt{\bigl(r(\cos\theta + \theta\sin\theta)^2 + r(\sin\theta - \theta\sin\theta)\bigr)^2} = r\sqrt{1+\theta^2}.$$

If the cow is tethered at $C = (-r,0)$ then the rope must have length $\pi r$, so that it can just reach the opposite point of the silo at $F = (r,0)$. The area available for grazing then consists of three parts:

• the area bounded by the arc of the involute from $F$ to $P = (-r,\pi r)$, the line $PC$ and the upper semicircle $CF$ of the silo;
• an equal area bounded by the arc of the involute from $F$ to $Q = (-r,-\pi r)$, the line $QC$ and the lower semicircle $CF$ of the silo;
• a semicircular area $PQG$ of radius $\pi r$.

The area of the semicircle is $\frac12\pi(\pi r)^2 = \frac12\pi^3r^2$. The combined area of the other two parts is given by the integral $$2\!\!\int_0^\pi\!\!\!\int_r^{r\sqrt{1+\theta^2}} \rho\,d\rho\, d\theta = \int_0^\pi\Bigl[\rho^2\Bigr]_r^{r\sqrt{1+\theta^2}}d\theta = \int_0^\pi r^2\theta^2\,d\theta = \tfrac13r^2\pi^3.$$

Thus the total grazing area is $\frac12\pi^3r^2 + \frac13\pi^3r^2 = \boxed{\frac56\pi^3r^2}.$