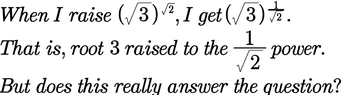Irrational Number Raised To Irrational Number

[nycmathguy]

Homework Statement

Can an irrational number raised to an irrational power yield an answer that is rational?

Relevant Equations

A = (sqrt{2})^(sqrt{2})

Can an irrational number raised to an irrational power yield an answer that is rational? This problem shows that
the answer is “yes.” (However, if you study the following solution very carefully, you’ll see that even though we’ve answered the question in the affirmative, we’ve not
pinpointed the specific case in which an irrational number raised to an irrational power is rational.)

(a) Let A = (sqrt{2})^(sqrt{2})
Now, either A is rational or A is irra-
tional. If A is rational, we are done. Why?

(b) If A is irrational, we are done. Why?
Hint Given: Consider A^(sqrt{2})

 

[Office_Shredder]

If it's rational, do you understand why you are done?

 

[PeroK]

Mathematics at times is so beautiful!

 

[Delta2]

In my opinion the specific case is that $A=\sqrt 2^{\sqrt 2}$ is irrational and when we raise this irrational to the irrational power of $\sqrt 2$ we get a rational that is $$A^{\sqrt 2}={\left (\sqrt 2^{(\sqrt 2)}\right )}^{\sqrt 2}=(\sqrt 2)^{(\sqrt 2)(\sqrt 2)}=(\sqrt 2)^2=2$$.

 

[nycmathguy]

If it's rational, do you understand why you are done?

No. This is why I posted this question.

 

[nycmathguy]

In my opinion the specific case is that $A=\sqrt 2^{\sqrt 2}$ is irrational and when we raise this irrational to the irrational power of $\sqrt 2$ we get a rational that is $$A^{\sqrt 2}={\left (\sqrt 2^{(\sqrt 2)}\right )}^{\sqrt 2}=(\sqrt 2)^{(\sqrt 2)(\sqrt 2)}=(\sqrt 2)^2=2$$.

This reply is your opinion but you are not really sure, right?

 

[nycmathguy]

Mathematics at times is so beautiful!

What does this have to do with (irrational)^(irrational)?

 

[Delta2]

This reply is your opinion but you are not really sure, right?

Yes I am not really sure as I can't provide a proof that $A$ is irrational.

 

[nycmathguy]

Yes I am not really sure as I can't provide a proof that $A$ is irrational.

Let me see if the answer is in the back of the book. If so, I will post here.

 

[nycmathguy]

In my opinion the specific case is that $A=\sqrt 2^{\sqrt 2}$ is irrational and when we raise this irrational to the irrational power of $\sqrt 2$ we get a rational that is $$A^{\sqrt 2}={\left (\sqrt 2^{(\sqrt 2)}\right )}^{\sqrt 2}=(\sqrt 2)^{(\sqrt 2)(\sqrt 2)}=(\sqrt 2)^2=2$$.

I just checked the book. This is an even number problem. The book does not provide answers, like most textbooks, to even number problems.

 

[Delta2]

Anyway we have two possible cases of (which one must be true):

1. A is rational. Then we are done because A is of the form (irrational)^(irrational)
2. A is not rational, that is A is irrational. Then we are done if we take the number $A^{\sqrt 2}$ which is of the form (irrational)^(irrational) (since A is irrational and $\sqrt 2$ is irrational too) and we can prove that $A^{\sqrt 2}$ is equal to 2 hence rational.

 

[nycmathguy]

In my opinion the specific case is that $A=\sqrt 2^{\sqrt 2}$ is irrational and when we raise this irrational to the irrational power of $\sqrt 2$ we get a rational that is $$A^{\sqrt 2}={\left (\sqrt 2^{(\sqrt 2)}\right )}^{\sqrt 2}=(\sqrt 2)^{(\sqrt 2)(\sqrt 2)}=(\sqrt 2)^2=2$$.

Anyway we have two possible cases of (which one must be true):

1. A is rational. Then we are done because A is of the form (irrational)^(irrational)
2. A is not rational, that is A is irrational. Then we are done if we take the number $A^{\sqrt 2}$ which is of the form (irrational)^(irrational) (since A is irrational and $\sqrt 2$ is irrational too) and we can prove that $A^{\sqrt 2}$ is equal to 2 hence rational.

See attachment.

 

[Delta2]

See attachment.

Well I am not sure if I understand well what you write at the attachment (you say when you raise $\sqrt{3}^{\sqrt 2}$ but you are not saying the power to which you are raising it to, I guess you mean 1/2).
But yes you can work with $A=\sqrt{3}^{\sqrt 2}$ instead .

 

[Delta2]

or $$\sqrt{3}^{\sqrt 2}=(3^{\frac{1}{2}})^{\sqrt 2}=3^{\frac{\sqrt 2}{2}}=3^{\frac{1}{\sqrt 2}}$$ if that was what you were trying to say.

 

[nycmathguy]

Well I am not sure if I understand well what you write at the attachment (you say when you raise $\sqrt{3}^{\sqrt 2}$ but you are not saying the power to which you are raising it to, I guess you mean 1/2).
But yes you can work with $A=\sqrt{3}^{\sqrt 2}$

or $$\sqrt{3}^{\sqrt 2}=(3^{\frac{1}{2}})^{\sqrt 2}=3^{\frac{\sqrt 2}{2}}=3^{\frac{1}{\sqrt 2}}$$ if that was what you were trying to say.

Correct but does this answer the question? I understand this problem not to be the typical precalculus classroom question but I find it interesting as given in the David Cohen book Edition 4.

 

[Delta2]

No this doesn't answer the question, you have to work with $A=3^{\frac{1}{\sqrt 2}}$ with similar logic as before, that is to take cases if A is rational or irrational (if it rational we are done, if it is irrational we take the number $A^{\sqrt 2}$ and we are done cause it is equal to 3.

 

[nycmathguy]

No this doesn't answer the question, you have to work with $A=3^{\frac{1}{\sqrt 2}}$ with similar logic as before, that is to take cases if A is rational or irrational (if it rational we are done, if it is irrational we take the number $A^{\sqrt 2}$ and we are done cause it is equal

Let me work on this some more.

 

[haruspex]

What does this have to do with (irrational)^(irrational)?

@PeroK is expressing pleasure in that elegant mathematical technique, the non-constructive proof. The problem as given does not require you to find a specific example, merely to show that there must be one.
https://en.m.wikipedia.org/wiki/Constructive_proof

Is your attachment in post #12 an attempt at a constructive proof?
There are numerous cases for which no constructive proof is known.

 

[Office_Shredder]

Let me work on this some more.

This problem, when you get it, is one of the simplest results in existence. I think mostly it requires just thinking about the words that are being used, and not like, doing actual work.

$\sqrt{2}$ is an irrational number. If we can find some other irrational number $x$ such that $x^\sqrt{2}$ is rational, then we have succeeded.One proposal is $x=\sqrt{2}$.

There are two possibilities.
1.) $\sqrt{2}^\sqrt{2}$ is rational. What is it that we wanted to be true in the first place? Do we have any more work left to do in this case?

2.) $\sqrt{2}^\sqrt{2}$ is irrational. Then we can just try $x=\sqrt{2}^\sqrt{2}$. What do we want to be true about that number?

 

[nycmathguy]

This problem, when you get it, is one of the simplest results in existence. I think mostly it requires just thinking about the words that are being used, and not like, doing actual work.

$\sqrt{2}$ is an irrational number. If we can find some other irrational number $x$ such that $x^\sqrt{2}$ is rational, then we have succeeded.One proposal is $x=\sqrt{2}$.

There are two possibilities.
1.) $\sqrt{2}^\sqrt{2}$ is rational. What is it that we wanted to be true in the first place? Do we have any more work left to do in this case?

2.) $\sqrt{2}^\sqrt{2}$ is irrational. Then we can just try $x=\sqrt{2}^\sqrt{2}$. What do we want to be true about that number?

1. We are done. No more work needed.

2. We want that number to be irrational.

 

[haruspex]

2. We want that number to be irrational.

No, "that number" is "$x=\sqrt{2}^\sqrt{2}$" and we are in case 2:

2.) $\sqrt{2}^\sqrt{2}$ is irrational

So we already know it is irrational.
There is another property we need it to have:

find some other irrational number $x$ such that $x^\sqrt{2}$ is rational,

 

[nycmathguy]

No, "that number" is "$x=\sqrt{2}^\sqrt{2}$" and we are in case 2:

So we already know it is irrational.
There is another property we need it to have:

If the number A is irrational, than A^sqrt(2) is rational. Yes?

Proof:

I know that sqrt[2] is irrational. So, if A=sqrt[2] and B=sqrt[2] satisfy the conclusion of the theorem, then I am done.
If they do not, then sqrt[2]^sqrt[2] is irrational, so I let A be this number.
Then, letting A=sqrt[2]^sqrt[2] and B=sqrt[2], it is easy for me to verify that A^B=2 which is rational and so would satisfy the conclusion of the theorem. This is my guess.

You say?

 

[WWGD]

How about the approach of raising x to the power $log_3 x$ or any other Rational base?

 

[Office_Shredder]

How about the approach of raising x to the power $log_3 x$ or any other Rational base?

How would you prove that's irrational to begin with?

If the number A is irrational, than A^sqrt(2) is rational. Yes?

Proof:

I know that sqrt[2] is irrational. So, if A=sqrt[2] and B=sqrt[2] satisfy the conclusion of the theorem, then I am done.
If they do not, then sqrt[2]^sqrt[2] is irrational, so I let A be this number.
Then, letting A=sqrt[2]^sqrt[2] and B=sqrt[2], it is easy for me to verify that A^B=2 which is rational and so would satisfy the conclusion of the theorem. This is my guess.

You say?

This looks good to me.

 

[haruspex]

This looks good to me.

Me too.

 

[Delta2]

Me too.

Me three.

 

[PeroK]

PS alternatively, of course, you can do a proof by contradiction:

Conjecture: any irrational raised to the power of an irrational is always irrational.

Therefore: $A = \sqrt 2^{\sqrt 2}$ is irrational, and likewise $A^{\sqrt 2}$ is irrational.

However, $A^{\sqrt 2} = 2$, which is a contradiction.

Conclusion: the original conjecture must be false.

 

[nycmathguy]

How would you prove that's irrational to begin with?This looks good to me.

Thank you. I took me a while to come up with this proof.

 

[WWGD]

How would you prove that's irrational to begin with?This looks good to me.

By contradiction. Assume $log_3 2=p/q$. Edit: Then $3^{p/q}=2$. Get rid of exponent... ( just a hint for OP).

 

[PeroK]

By contradiction. Assume $log_3 2=p/q$. Then $2^{p/q}=3$. Get rid of exponent... ( just a hint for OP).

Or, perhaps, $3^{p/q} = 2$?