Irreversible adiabatic processes & entropy change (clarification needed)

[Juanda]

TL;DR Summary

A different thread was posted and I couldn't understand it. I was recommended to open a new thread to keep the original one on track.

Last month @Chestermiller opened the thread: Focus Problem for Entropy Change in Irreversible Adiabatic Process.
I couldn't wrap my head around something apparently simple but the thread was not about that so I was instructed to open a new thread to discuss it separately and keep the original thread on track.
I owned this thread to Chestermiller for a while now and finally, I have the chance to open it.

I'll copy and paste the same problem statement only changing the instant drop in external pressure with the piston being released from some braking system which is easier for me to visualize and I believe should have the same consequences.

I have an ideal gas in a cylinder with a massless, frictionless piston, and the gas starts out at To, Po, Vo. The system is adiabatic. The gas is in equilibrium at Po because the piston is held in place by a braking system. I initiate an irreversible process by releasing the brakes so the piston is exposed to the lower external pressure P1 which is constant while the gas expands and equilibrates with the new external pressure P1 at a new volume and temperate V1 and T1.

(a) Based on the 1st law of thermodynamics and the ideal gas law, what are the values of the new volume and temperature (in terms of Po, To, Vo, and P1)? How much irreversible work was done? What was the change in U?

(b) Describe at least 2 reversible processes you have devised to transition from the same initial state to the same final state. How much work was done, how much heat was added in each, and what was the change in U for these reversible processes?

(c). What was the change in entropy for the reversible processes? What was the change in entropy of the irreversible process?

So the problem has 3 questions (a, b, and c) although I'm already stuck in the first one. Mathematically I think I can find the state 1 ($P_1$, $T_1$ and $V_1$) when the external and internal pressures are the same ($P_0$ expands towards $P_1$) using the adiabatic process relation because it's an adiabatic system so it should be an adiabatic expansion and the ideal gas law.
$$P_0V_0^\gamma=P_1V_1^\gamma \rightarrow V_1=e^\frac{\ln \frac{P_0V_0^\gamma}{P_1}}{\gamma} \tag{1}$$
$$P_1V_1=mRT_1 \rightarrow T_1 = \frac{P_1V_1}{mR} \tag{2}$$

But I don't see how the system can be in equilibrium when it reaches that point.

The way I see it, the work done by the adiabatic expansion of the gas inside the piston must be equal to the work done in the isobaric compression of the gas outside the piston because energy has no other place to go since heat transfer is not allowed (adiabatic system) and any other path for energy has been restricted (frictionless, massless, etc.).
The gas inside the piston will expand until its pressure levels with the outside pressure (P0→P1).
The energy required for such expansion would come from the internal energy of the gas inside the piston which can be expressed as a function of temperature (ideal gas).
However, I don't see how those two Works (adiabatic expansion in the piston and isobaric expansion outside) can be the same.

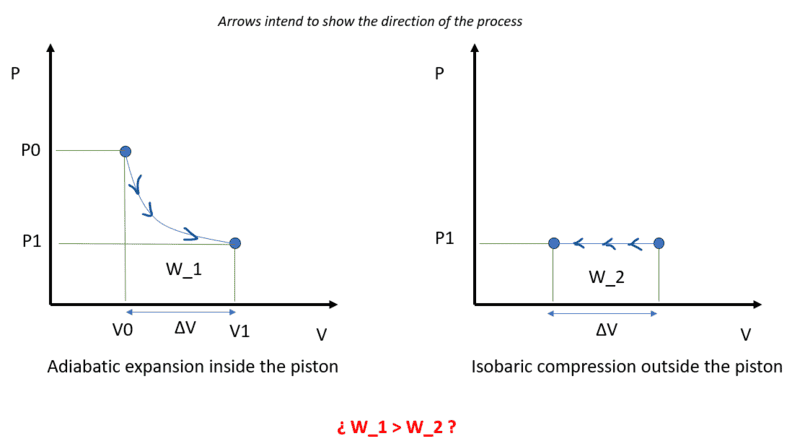
I'd need to include something else. For example, if the piston had mass, the difference in Works would be absorbed as kinetic energy of the piston and would be $K_p = W_1-W_2$. In that case, the piston would reach the equilibrium point with non-zero velocity so it would overshoot and an oscillating movement would start. With friction being removed from the problem as the statement declares, the oscillation would keep going indefinitely.

This differs a lot when compared with what was done in the original thread. For example, Vanhees71 used the thermal energy in the gas to match the isobaric compression of the outside gas but I don't understand why it's possible to do that if it's been established that the piston undergoes an adiabatic expansion.

PS: On a little unrelated note. I have trouble understanding the units in equation $(1)$. On the left side, we have units for volume $[m^3]$ as expected but on the right side, after doing some simplifications I arrive at $[m^3]^\gamma$. Is that OK? I don't see how $[m^3]=[m^3]^\gamma$. I am aware of \gamma being unitless but still has an impact on the equation.

 

[Chestermiller]

In your judgment, in a rapid irreversible expansion of an ideal gas within your cylinder, does the ideal gas satisfy the ideal gas law PV=nRT throughout the expansion? (Is the force per unit area exerted by an ideal gas on the inside face of the piston equal to the pressure P calculated from the ideal gas law in an irreversible expansion?). Does an ideal gas satisfy the ideal gas law only at thermodynamic equilibrium states, or for all states, including non-thermodynamic equilibrium states?

In the case where you have a frictionless piston with mass, does the piston oscillate forever, or is there something besides dry friction present that damps the piston motion and eventually stops it?

Are you familiar with Newton's law of viscosity in 3D, involving the stress tensor and the velocity gradient tensor? (Wiki)

 

[Juanda]

In your judgment, in a rapid irreversible expansion of an ideal gas within your cylinder, does the ideal gas satisfy the ideal gas law PV=nRT throughout the expansion? (Is the force per unit area exerted by an ideal gas on the inside face of the piston equal to the pressure P calculated from the ideal gas law in an irreversible expansion?). Does an ideal gas satisfy the ideal gas law only at thermodynamic equilibrium states, or for all states, including non-thermodynamic equilibrium states?

Whenever working on problems with pistons like this I assume quasi-equilibrium in the gas. Is that not recommended here? If it is in quasi-equilibrium it means it is evolving while going through equilibrium states so I believe PV=mRT should always be true.
If the piston's face moves so quickly that it leaves a vacuum behind when expanding or an area of greater pressure when contracting then I guess the equation is no longer valid to describe the whole gas inside the piston during the process. I believe the formula should work again when the piston is stopped though as the gas adapts to the available volume and changes its pressure and temperature accordingly to again fall in PV=mRT.

(I'm interchanging n and m. The concept of mols always leaves me confused. As long as the right version of R is used there should be no problem. If you prefer me to use n from now on I'll use it.)

In the case where you have a frictionless piston with mass, does the piston oscillate forever, or is there something besides dry friction present that damps the piston motion and eventually stops it?

Are you familiar with Newton's law of viscosity in 3D, involving the stress tensor and the velocity gradient tensor?

I didn't see the viscosity of the gas as a possibility in this problem although I now realize that might have been the main point from the beginning. I haven't worked so closely with fluids in quite a while but I understand the losses due to viscosity are related to the different velocities in it and the shear that appears between "layers". I hope a conceptual understanding of that is enough to understand the expansion being discussed here.

So, in an ideal case, the expansion would have been adiabatic and would have produced $W_1$. However, the produced work will be lower because there are losses due to the viscosity of the fluid. The difference in area between the ideal path and the actual path would be the losses due to the friction in the fluid. Such losses will produce heat but it cannot escape the system because it's adiabatic. What will happen to that heat then? Will it be stored as thermal energy in the gas? Can we even call it losses if it's not being lost anywhere?

Also, work produced during the expansion depends on the PV curve of the gas inside the piston. How can we then know what's the PV curve that the gas follows during 0→1? Does it even make sense to plot such a curve if the gas no longer follows PV=mRT because of the rapid expansion?

 

[Chestermiller]

Whenever working on problems with pistons like this I assume quasi-equilibrium in the gas. Is that not recommended here?

No. The deformation is occurring rapidly, the the expansion is irreversible here./

it is in quasi-equilibrium it means it is evolving while going through equilibrium states so I believe PV=mRT should always be true.

The ideal gas law is valid only for a thermodynamic equilibrium state (or a for a reversible process, which is comprised of a continuous sequence of thermodynamic equilibrium states). A real gas equation of state (e.g., Van Der Waals EOS) is valid only for a thermodynamic equilibrium state (or a for a reversible process, which is comprised of a continuous sequence of thermodynamic equilibrium states). Otherwise they give the wrong answer for the force of the gas on the piston.

If the piston's face moves so quickly that it leaves a vacuum behind when expanding or an area of greater pressure when contracting then I guess the equation is no longer valid to describe the whole gas inside the piston during the process. I believe the formula should work again when the piston is stopped though as the gas adapts to the available volume and changes its pressure and temperature accordingly to again fall in PV=mRT.

It isn't exactly a vacuum. Viscous stresses (which can be negative) reduces the normal stress on the piston. The normal stress depends not only on the volume, but also on the rate of change of volume.

I didn't see the viscosity of the gas as a possibility in this problem although I now realize that might have been the main point from the beginning. I haven't worked so closely with fluids in quite a while but I understand the losses due to viscosity are related to the different velocities in it and the shear that appears between "layers". I hope a conceptual understanding of that is enough to understand the expansion being discussed here.

Even for a gas undergoing shear between layers, the deformation can be resolved into pure extension at+ 45 degrees to the layers, and pure compression at -45 degrees to the layers. So viscosity doesn't only come into play with shear between layers, but, more generally, with extension (like normal to the piston face). This causes a negative contribution to the compressive force on the piston if it is moving fast enough.

So, in an ideal case, the expansion would have been adiabatic and would have produced $W_1$. However, the produced work will be lower because there are losses due to the viscosity of the fluid. The difference in area between the ideal path and the actual path would be the losses due to the friction in the fluid. Such losses will produce heat but it cannot escape the system because it's adiabatic. What will happen to that heat then? Will it be stored as thermal energy in the gas? Can we even call it losses if it's not being lost anywhere?

There is less work done by the gas on the piston (because the normal force is less than in irreversible) and less change in internal energy.

Also, work produced during the expansion depends on the PV curve of the gas inside the piston. How can we then know what's the PV curve that the gas follows during 0→1? Does it even make sense to plot such a curve if the gas no longer follows PV=mRT because of the rapid expansion?

Super question. Of course, if the piston is massless and frictionless, then the work done by the gas is equal to the imposed external pressure integrated over the volume change (since the gas normal force must equal the imposed external pressure times the piston area). If the external pressure is not known (i.e., specifically imposed as a function of volume), then we need to solve the detailed partial differential equation of fluid mechanics and partial differential equation of thermal energy in conjunction with the continuity equation (differential equation of mass balance), subject to the Imposed boundary conditions for velocity and heat flux at the cylinder and piston surfaces. This requires the use of computational fluid dynamics.

 

[Juanda]

I think I just visualized how the gas is expanding in the "real case". Since the piston has almost no inertia because it's very light, once the brakes are released it expands very quickly towards the new equilibrium pressure. Again, since there is almost no inertia, it'll overshoot but as soon as it does so it oscillates very quickly around that point dissipating the energy through the viscosity of the fluid.
The force at the piston's face in such a scenario can only be derived through CFD.

Now, coming back to the original ideal problem where it's a massless piston going through an adiabatic irreversible expansion with constant pressure outside the piston. The total work done by the gas pushing inside the piston must be $W_2=P_1 \Delta V$ (nomenclature from the picture) because that's the work that has been done on the atmosphere by the piston and energy has no other place to go. Using $PV^\gamma$ to find State 1 is not an option because that's only in quasi-equilibrium processes. Only the beginning and end (0 and 1) are in equilibrium. The process 0→1 is not.
Vanhees used the internal energy to find State 1 from State 0. Is that OK even if we're not considering quasi-equilibrium processes as we said before? He did it with N but I prefer m as I find it less confusing.
$$\Delta U=\cancel{Q}-W \rightarrow mc_v(T_1-T_0)=-P_1(V_1-V_0) \tag{1}$$
$$P_1V_1=mRT_1 \tag{2}$$
From $(1)$ and $(2)$ it is possible to obtain $T_1$ and $V_1$ from the known values. I didn't input numbers yet but I assume the temperature will not drop as much during this expansion when compared with the reversible adiabatic expansion so the outputting work is lower.

We could talk about some expansion efficiency like $\eta =\frac{W_1-W_2}{W_1}$ where $W_1$ would be the work done in the reversible adiabatic expansion. Always $W_1>W_2$ so the efficiency is lower than 1 as expected.

Something that feels strange to me is that even if we're not considering the PV curve of the gas inside the piston, by using that expression of work it's equivalent to say that the piston is undergoing an isobaric expansion.

 

[Chestermiller]

I think I just visualized how the gas is expanding in the "real case". Since the piston has almost no inertia because it's very light, once the brakes are released it expands very quickly towards the new equilibrium pressure. Again, since there is almost no inertia, it'll overshoot but as soon as it does so it oscillates very quickly around that point dissipating the energy through the viscosity of the fluid.
The force at the piston's face in such a scenario can only be derived through CFD.

Yes, except for the last sentence. If we do a force balance on the massless piston during this irreversible deformation, we obtain $$\frac{F_g(t)}{A}=P_{ext}(t)$$where $F_g(t)$ is the force of the gas on the inside face of the piston at time t during the expansion, A is the piston area, and $P_{ext}(t)$ is the external force per unit area at time t during the expansion. If we control the external pressure such that it is constant or a known function of the volume, then the force of the gas on the inside face of the piston $F_g$ and the deformation of the gas and viscous stresses within the cylinder will automatically adjust to match the external pressure. Under such circumstances, CFD will not have to be used. The work done by the gas will be $\int{P_{ext}dV}=\int{\frac{F_g}{A}dV}$, and can be calculated. However, it the external pressure is not constant or uncontrolled as a result of some other interaction with the surroundings, CFD would need to be used.

Now, coming back to the original ideal problem where it's a massless piston going through an adiabatic irreversible expansion with constant pressure outside the piston. The total work done by the gas pushing inside the piston must be $W_2=P_1 \Delta V$ (nomenclature from the picture) because that's the work that has been done on the atmosphere by the piston and energy has no other place to go. Using $PV^\gamma$ to find State 1 is not an option because that's only in quasi-equilibrium processes. Only the beginning and end (0 and 1) are in equilibrium. The process 0→1 is not.
Vanhees used the internal energy to find State 1 from State 0. Is that OK even if we're not considering quasi-equilibrium processes as we said before?

Yes. Internal energy is a function of state, so only the initial and final equilibrium states matter.

He did it with N but I prefer m as I find it less confusing.
$$\Delta U=\cancel{Q}-W \rightarrow mc_v(T_1-T_0)=-P_1(V_1-V_0) \tag{1}$$
$$P_1V_1=mRT_1 \tag{2}$$
From $(1)$ and $(2)$ it is possible to obtain $T_1$ and $V_1$ from the known values. I didn't input numbers yet but I assume the temperature will not drop as much during this expansion when compared with the reversible adiabatic expansion so the outputting work is lower.

I look it in the opposite sense. Since the work is lower, the temperature will not drop as much.

We could talk about some expansion efficiency like $\eta =\frac{W_1-W_2}{W_1}$ where $W_1$ would be the work done in the reversible adiabatic expansion. Always $W_1>W_2$ so the efficiency is lower than 1 as expected.

It is impossible to have a reversible adiabatic expansion between the same two states as an irreversible adiabatic expansion. Part of the reversible process would have to be non-adiabatic. Can you figure out why?

Something that feels strange to me is that even if we're not considering the PV curve of the gas inside the piston, by using that expression of work it's equivalent to say that the piston is undergoing an isobaric expansion.

I explained that above. The viscous stresses inside the cylinder and the piston velocity will automatically adjust to give a gas force on the piston face matching the isobaric external pressure.

 

[Juanda]

Yes, except for the last sentence. If we do a force balance on the massless piston during this irreversible deformation, we obtain $$\frac{F_g(t)}{A}=P_{ext}(t)$$where $F_g(t)$ is the force of the gas on the inside face of the piston at time t during the expansion, A is the piston area, and $P_{ext}(t)$ is the external force per unit area at time t during the expansion. If we control the external pressure such that it is constant or a known function of the volume, then the force of the gas on the inside face of the piston $F_g$ and the deformation of the gas and viscous stresses within the cylinder will automatically adjust to match the external pressure. Under such circumstances, CFD will not have to be used. The work done by the gas will be $\int{P_{ext}dV}=\int{\frac{F_g}{A}dV}$, and can be calculated. However, it the external pressure is not constant or uncontrolled as a result of some other interaction with the surroundings, CFD would need to be used.

I see how the equation you show forces that to happen. But why is that the case physically? What's making the viscous stress automatically act in such a way that the forces on both faces of the piston are balanced? That's what I meant with this in the previous post.

Post #5 at the end of it
Something that feels strange to me is that even if we're not considering the PV curve of the gas inside the piston, by using that expression of work it's equivalent to say that the piston is undergoing an isobaric expansion.

It is impossible to have a reversible adiabatic expansion between the same two states as an irreversible adiabatic expansion. Part of the reversible process would have to be non-adiabatic. Can you figure out why?

I think I know what you mean. The state 0 is defined from the initial conditions. From state 1 only the pressure is defined initially. I realized that state 1 ($P_1 \ V_1 \ T_1$) depends on the process to get there because even if we fix $P_1$, the final volumes $V_1$ and temperatures $T_1$ will be dependent on the kind of expansion happening. According to the math we are discussing the adiabatic reversible expansion ($PV^\gamma=cte$) will cool further producing more work than the irreversible process being considered (isobaric expansion) where the gas will not cool that much and will produce less work. I'm not certain if they expand up to the same volume though. I believe not, but I'd need to compare the different processes with the equations to be sure of which process expands further. I'll try to do it before the day after tomorrow.
So to actually have a valid "comparison" to see the efficiency of the expansion it would be necessary to compare the processes $0 \rightarrow 1_{adiab-rev}$ VS $0 \rightarrow 1_{adiab-irrev_{(isob)}}$ where the state 1 is different in each case since it depends on the process to get there.

 

[Chestermiller]

I see how the equation you show forces that to happen. But why is that the case physically? What's making the viscous stress automatically act in such a way that the forces on both faces of the piston are balanced? That's what I meant with this in the previous post.

There is no other choice. The velocity of the piston as a function of time will cause the viscous stresses within the gas to vary in such a way that the normal force of the gas on the inside face of the piston must match the external force variation.

I think I know what you mean. The state 0 is defined from the initial conditions. From state 1 only the pressure is defined initially. I realized that state 1 ($P_1 \ V_1 \ T_1$) depends on the process to get there because even if we fix $P_1$, the final volumes $V_1$ and temperatures $T_1$ will be dependent on the kind of expansion happening. According to the math we are discussing the adiabatic reversible expansion ($PV^\gamma=cte$) will cool further producing more work than the irreversible process being considered (isobaric expansion) where the gas will not cool that much and will produce less work. I'm not certain if they expand up to the same volume though. I believe not, but I'd need to compare the different processes with the equations to be sure of which process expands further. I'll try to do it before the day after tomorrow.
So to actually have a valid "comparison" to see the efficiency of the expansion it would be necessary to compare the processes $0 \rightarrow 1_{adiab-rev}$ VS $0 \rightarrow 1_{adiab-irrev_{(isob)}}$ where the state 1 is different in each case since it depends on the process to get there.

In the irreversible adiabatic expansion, entropy is generated within the gas, and the entropy of the gas is higher in state 1 than in state 0. In a reversible adiabatic expansion, the entropy of the gas is the same in the initial and final states. So the two final states can never match.

 

[Chestermiller]

I see how the equation you show forces that to happen. But why is that the case physically? What's making the viscous stress automatically act in such a way that the forces on both faces of the piston are balanced? That's what I meant with this in the previous post.

Suppose you have a viscous Newtonian fluid between two horizontal parallel plates, with the lower plate stationary and the upper plate capable of siding horizontally. You apply a shear force F to the upper plate and allow the system to shear until it attains a steady state velocity distribution (velocity varying linearly from 0 at the lower plate to V at the upper plate. The velocity V will adjust to ultimately attain a value such that the shear force exerted by the fluid on the upper plate matches the imposed shear force F: $$\eta\frac{V}{h}A=F$$where $\eta$ is the fluid viscosity, h is the spacing of the plates, and A is the plate area. This is just a simple example to give you an idea of how it plays out.

 

[Chestermiller]

We could talk about some expansion efficiency like $\eta =\frac{W_1-W_2}{W_1}$ where $W_1$ would be the work done in the reversible adiabatic expansion. Always $W_1>W_2$ so the efficiency is lower than 1 as expected.

This is an incorrect conclusion. In the other thread we showed that, depending on the reversible path, the reversible work between the same two end states as the irreversible process can be less than the irreversible work. In fact there are paths for which it can even have the opposite sign,

But the entropy changes are the same for all paths.

 

[Juanda]

There is no other choice. The velocity of the piston as a function of time will cause the viscous stresses within the gas to vary in such a way that the normal force of the gas on the inside face of the piston must match the external force variation.

------------------------------------------------------------------------------------------------------------------------------

Suppose you have a viscous Newtonian fluid between two horizontal parallel plates, with the lower plate stationary and the upper plate capable of siding horizontally. You apply a shear force F to the upper plate and allow the system to shear until it attains a steady state velocity distribution (velocity varying linearly from 0 at the lower plate to V at the upper plate. The velocity V will adjust to ultimately attain a value such that the shear force exerted by the fluid on the upper plate matches the imposed shear force F:
$$\eta\frac{V}{h}A=F$$
where $\eta$ is the fluid viscosity, h is the spacing of the plates, and A is the plate area. This is just a simple example to give you an idea of how it plays out.

I think the problem I'm having is that removing the piston's mass is messing with my head. You mention yourself how there'll be a period of time before the plate reaches the stationary velocity (or so close to it that it's indistinguishable).
With the piston, are we assuming it reaches that stationary velocity instantly so the forces in both faces must be the same? Is that assumption close to reality or an idealization? My very limited experience with pistons induced me to believe that the piston will just keep on accelerating as long as the pressure inside is greater and once it goes beyond the equilibrium point the acceleration will become negative.

In the irreversible adiabatic expansion, entropy is generated within the gas, and the entropy of the gas is higher in state 1 than in state 0. In a reversible adiabatic expansion, the entropy of the gas is the same in the initial and final states. So the two final states can never match.

That's definitely more concise than what I was trying to express. I tend to avoid relying on $u \ h \ s$ even without realizing it because they are harder to imagine although they are just as fundamental (maybe with the exception of h which be derived from others and is just convenient to use in some cases).

This is an incorrect conclusion. In the other thread we showed that, depending on the reversible path, the reversible work between the same two end states as the irreversible process can be less than the irreversible work. In fact there are paths for which it can even have the opposite sign,

But the entropy changes are the same for all paths.

Let's see if I got it. Entropy may change when going from state 0 to state 1 (0→1). Such change can be due to the entropy being generated or because the entropy comes into or leaves the system (the gas inside the piston).
If the entropy was not generated, then the process is reversible because undoing it will produce/require the same work. Is it like that? That's why there can be multiple paths connecting the two states. For example, in an isobaric expansion if the entropy change is only due to heat absorption then the path is reversible, and the equation PV=mRT can be used throughout the full path.

 

[Chestermiller]

I think the problem I'm having is that removing the piston's mass is messing with my head. You mention yourself how there'll be a period of time before the plate reaches the stationary velocity (or so close to it that it's indistinguishable).
With the piston, are we assuming it reaches that stationary velocity instantly so the forces in both faces must be the same? Is that assumption close to reality or an idealization? My very limited experience with pistons induced me to believe that the piston will just keep on accelerating as long as the pressure inside is greater and once it goes beyond the equilibrium point the acceleration will become negative.

No, but you are very perceptive. Let's look at the case of the fluid between parallel plates to get a notion of what happens during the transient period. If we assume that the upper plate is massless (like the massless piston), then, at the instant that the shear force F is applied to the plate, the shear stress within the fluid immediately adjacent to the plate will instantly jump to the shear force F divided by the plate area A, and stay at that value for all times: $$\sigma=F/A$$The plate does not have inertia (mass), but the fluid below does have inertia (mass), so it will not all instantly attain the steady state profile $v=\frac{F}{A}\frac{1}{\eta}y$. Instead, to an excellent approximation, a "momentum boundary layer" of thickness $\delta(t)$ will develop in the region immediately adjacent to the upper plate. At distances below the plate where $y<h-\delta (t)$ the fluid will not have moved yet, but at distances closer to the plate, the fluid velocity will vary linearly with position through the boundary layer, such that $$v(y,t)=\frac{1}{\eta}\frac{F}{A} [y-(h-\delta)]=\frac{1}{\eta}\frac{F}{A}\delta\left[1-\frac{(h-y)}{\delta}\right]$$According to this, the velocity of the fluid at the plate (and the plate velocity) will be $$V(t)=\frac{1}{\eta}\frac{F}{A}\delta(t)$$When the boundary thickness has grown to the spacing between the plates (i.e., $\delta (t)=h$), the steady state velocity profile (and steady state plate velocity) will be attained: $$V=\frac{1}{\eta}\frac{F}{A}h$$The solution to the fluid dynamic equations shows that the momentum boundary layer thickness will grow in proportion to $\sqrt{t}$: $$\delta(t)=k\sqrt{\nu t}$$where $\nu$ is the kinematic viscosity.

The same kind of scenario will play out with the gas and piston. Immediately after the piston pressure drops to $P_{ext}$, the compressive stress within the gas at the piston face will also drop to $P_{ext}$. A viscous momentum boundary layer will develop in the region adjacent to the piston with a thickness $\delta(t)$ that grows with time. At short times, the massless piston velocity will also grow with time, and will be proportional to the boundary layer thickness.

Let's see if I got it. Entropy may change when going from state 0 to state 1 (0→1). Such change can be due to the entropy being generated or because the entropy comes into or leaves the system (the gas inside the piston).
If the entropy was not generated, then the process is reversible because undoing it will produce/require the same work.

Not work. To attain the same entropy change reversibly will require heat addition (and is non-adiabatic)

Is it like that? That's why there can be multiple paths connecting the two states. For example, in an isobaric expansion if the entropy change is only due to heat absorption then the path is reversible, and the equation PV=mRT can be used throughout the full path.

I don't understand this statement.

 

[Juanda]

According to this, the velocity of the fluid at the plate (and the plate velocity) will be $$V(t)=\frac{1}{\eta}\frac{F}{A}\delta(t)$$When the boundary thickness has grown to the spacing between the plates (i.e., $\delta (t)=h$), the steady state velocity profile (and steady state plate velocity) will be attained: $$V=\frac{1}{\eta}\frac{F}{A}h$$The solution to the fluid dynamic equations shows that the momentum boundary layer thickness will grow in proportion to $\sqrt{t}$: $$\delta(t)=k\sqrt{\nu t}$$where $\nu$ is the kinematic viscosity.

I couldn't find the meaning of $k$. Is it just an arbitrary constant from experimentation or maybe the initial thickness of the boundary layer attached to the plate?
Anyways I followed the math and I think I get it. I mean for the plate. The piston is still rocking in my head.

The same kind of scenario will play out with the gas and piston. Immediately after the piston pressure drops to $P_{ext}$, the compressive stress within the gas at the piston face will also drop to $P_{ext}$. A viscous momentum boundary layer will develop in the region adjacent to the piston with a thickness $\delta(t)$ that grows with time. At short times, the massless piston velocity will also grow with time, and will be proportional to the boundary layer thickness.

I'm having a very hard time trying to understand the piston scenario. Maybe the following makes sense. Something that drops from that argument is that, no matter how much pressure we had built in the gas, once the brakes are released, if the pistons' inertia is too low for the gas inside to keep up with its movement, the pressure will instantly drop to $P_1$ at the inner face of the piston and from there it'll expand at a constant velocity with the pressure at the inner and outer faces being equal. So it's kind of an isobaric expansion at $P_1$.

I don't understand this statement.

What I meant to say is that as long as PV=mRT is true for a given path A→B for the whole chamber then the process is reversible no matter the path. Even if heat is added or removed during the process as long as entropy is not generated.

 

[Chestermiller]

I couldn't find the meaning of $k$. Is it just an arbitrary constant from experimentation or maybe the initial thickness of the boundary layer attached to the plate?
Anyways I followed the math and I think I get it. I mean for the plate. The piston is still rocking in my head.

It follows from the Navier Stokes equations that the velocity satisfies:
$$\frac{\partial v}{\partial t}=\nu\frac{\partial^2 v}{\partial y^2}$$If we integrate this equation with respect to y between $(h-\delta)$ and h, we obtain:$$\frac{\partial \int_{h-\delta}^h{v dy}}{\partial t}=\left[\frac{\partial v}{\partial y}\right]_{y=h}$$If we substitute our approximate equation for v(y,t) into this equation, we obtain $$\frac{d\delta^2}{2dt}=\nu$$which then integrates to $$\delta=\sqrt{2\nu t}$$

I'm having a very hard time trying to understand the piston scenario. Maybe the following makes sense. Something that drops from that argument is that, no matter how much pressure we had built in the gas, once the brakes are released, if the pistons' inertia is too low for the gas inside to keep up with its movement, the pressure will instantly drop to $P_1$ at the inner face of the piston and from there it'll expand at a constant velocity with the pressure at the inner and outer faces being equal. So it's kind of an isobaric expansion at $P_1$.

It won't expand at constant piston velocity, just as in the case of the upper plate in the shear scenario. The piston will start off at zero velocity at time zero, and the velocity will grow with time. However, this does not mean that the local extension rate of the gas at the piston face is zero at time zero, since the thickness at the boundary layer will also zero. The limit of the piston velocity divided by the boundary layer thickness is finite. This allows a finite viscous stress at the piston, and allows the gas force on the piston to drop from PoA to $P_1A$.

What I meant to say is that as long as PV=mRT is true during the path 0→1 for the whole chamber then the process is reversible no matter the path. Even if heat is added or removed during the process as long as entropy is not generated.

No, it does not depend on PV=mRT. It depends on the deformation being such that no entropy is generated.

 

[Juanda]

It won't expand at constant piston velocity, just as in the case of the upper plate in the shear scenario. The piston will start off at zero velocity at time zero, and the velocity will grow with time. However, this does not mean that the local extension rate of the gas at the piston face is zero at time zero, since the thickness at the boundary layer will also zero. The limit of the piston velocity divided by the boundary layer thickness is finite. This allows a finite viscous stress at the piston, and allows the gas force on the piston to drop from PoA to $P_1A$.

So the inner face of the piston is under $P_1A$ because the viscous stress causes a drop in pressure at the inner face of the piston. The pressure on the inner face is the same as the pressure on the outer face. No more forces are acting on the piston. How is the velocity not constant? The sum of forces is zero so the acceleration should be 0. Am I missing any force on it?

No, it does not depend on PV=mRT. It depends on the deformation being such that no entropy is generated.

Is it then possible to have an ideal gas expanding where entropy is not generated AND $PV \neq mRT$ along the path?

 

[Chestermiller]

So the inner face of the piston is under $P_1A$ because the viscous stress causes a drop in pressure

Pressure is the isotropic part of the compressive stress tensor. This is not the force per unit area exerted by the gas on the inside face of the piston during an irreversible deformation. The compressive stress exerted by the gas on the inside face of the piston is: $$\sigma=p-\tau$$where $\tau$ is the viscous contribution to the compressive stress. See Transport Phenomena by Bird, Stewart, and Lightfoot, Chapter 1, Section 1.2

at the inner face of the piston. The pressure on the inner face is the same as the pressure on the outer face.

Again, the compressive stress on the inner face is the same as the pressure on the outer face.

How is the velocity not constant? The sum of forces is zero so the acceleration should be 0. Am I missing any force on it?

If the mass is zero, it doesn't matter what the acceleration is. The two forces are equal. In order for this to happen, the gas near the inside face must be deforming rapidly enough, and that requires the piston velocity divided by the boundary layer thickness to approach the required viscous stress divided by the gas viscosity in the limit of short times.

Is it then possible to have an ideal gas expanding where entropy is not generated AND $PV \neq mRT$ along the path?

Sure, in a reversible expansion. But, the key criterion is no entropy generation, not PV=mRT. If the expansion is reversible, then PV=mRT follows, not leads. The thought sequence should be:

1. I have a reversible process. A reversible process consists of a continuous sequence of thermodynamics equilibrium states. I can use the ideal gas law (or other real gas equation of state) for a thermodynamic equilibrium state only. I can use the ideal gas law for a reversible process.

2. I have an irreversible process. An irreversible process does not consist of a continuous sequence of thermodynamics equilibrium states. I can use the ideal gas law (or other real gas equation of state) for a thermodynamic equilibrium state only. I can not use the ideal gas law for a irreversible process, except for the initial and final states if these are thermodynamic equilibrium states..

 

[Juanda]

All right. Thanks a lot for the extra explanations. I'll try to read again the original thread where you posted the problem and try to understand it.

 

[Chestermiller]

All right. Thanks a lot for the extra explanations. I'll try to read again the original thread where you posted the problem and try to understand it.

Also please please please read the reference I identified.

Chet

 

[Juanda]

Also please please please read the reference I identified.

Chet

I quickly skipped through both threads and I'm not certain of which reference you mean. Many things were said and I can't identify which is the one you consider to be especially important.
Did you mean I should read the threads carefully? I will certainly do that. I'm preparing for a trip now so I might be inactive for a few days but it's definitely on the list.
Or did you mean a specific paper or article? Do you mind resharing it?

 

[Chestermiller]

Transport Phenomena by Bird, Stewart, and Lightfoot

1. Chapter 1, Section 1.2, Generalizaation of Newton's Law of Viscosity

2. Chapter 11, homework problem 11.D.1, Equation for change of entropy

 

[Juanda]

Transport Phenomena by Bird, Stewart, and Lightfoot

1. Chapter 1, Section 1.2, Generalizaation of Newton's Law of Viscosity

2. Chapter 11, homework problem 11.D.1, Equation for change of entropy

I did read and reread both references you mentioned.

It proved this is just too advanced for me to grasp now. I'm biting more than I can chew.

I'm currently reading what I consider to be a far simpler book (Thermodynamics An Engineering Approach by Çengel, Boles, and Kanoglu 10th Ed) which mostly covers things I already studied quite a while ago and still I'm struggling with it at some points.
To be honest, I'm not being able to dedicate as much time to studying it as I'd like but I'll try to finish it and maybe it'll give me some insight about this thread and the references you provided.

 

[Chestermiller]

I did read and reread both references you mentioned.
View attachment 331139
View attachment 331138

It proved this is just too advanced for me to grasp now. I'm biting more than I can chew.

I'm currently reading what I consider to be a far simpler book (Thermodynamics An Engineering Approach by Çengel, Boles, and Kanoglu 10th Ed) which mostly covers things I already studied quite a while ago and still I'm struggling with it at some points.
To be honest, I'm not being able to dedicate as much time to studying it as I'd like but I'll try to finish it and maybe it'll give me some insight about this thread and the references you provided.

Don't feel too bad. Even after having had courses in fluid mechanics, transport phenomena, and thermodynamics as a senior in college and as a first year graduate student, I never made the connection between viscous dissipation of mechanical energy and entropy generation. It wasn't until many decades later, after my engineering career was over and as a Mentor in Physics Forums that I came across problem 11.D.1 in transport phenomena and it all clicked. I also came across Fundamentals of Engineering Thermodynamics by Moran et al (Chapter 6) where other aspects of entropy change became apparent to me:

For a closed system, there are only two ways that the entropy of the system can change:

1. By entropy generation within the system as a result of irreversibility. This is caused by transport processes proceeding within the system at finite rates: viscous dissipation (by rapid deformation) at finite velocity gradients, internal heat conduction at finite temperature gradients, and molecular diffusion at finite concentration gradients. This, together with the fundamental distinction between the isotropic stress tensor for an inviscid fluid (characterized purely in terms of the thermodynamic pressure P) and anisotropic contribution to the stress tensor of a viscous fluid deforming due to local velocity gradients explains why P is not the compressive stress component at the inside piston face in a rapid irreversible process.

2. By entropy transfer between the surroundings to the system (across the boundary between the system and surroundings) as a result of heat flow across the boundary, at the boundary temperature: $\int{dQ/T_B}$. This mechanism can be present in both reversible- and irreversible processes. In a reversible process, it is the only mechanism present.

Understanding these two mechanisms is virtually all you really need to know.

 

[Andrew Mason]

I have an ideal gas in a cylinder with a massless, frictionless piston, and the gas starts out at To, Po, Vo. The system is adiabatic. The gas is in equilibrium at Po because the piston is held in place by a braking system. I initiate an irreversible process by releasing the brakes so the piston is exposed to the lower external pressure P1 which is constant while the gas expands and equilibrates with the new external pressure P1 at a new volume and temperate V1 and T1.

(a) Based on the 1st law of thermodynamics and the ideal gas law, what are the values of the new volume and temperature (in terms of Po, To, Vo, and P1)? How much irreversible work was done? What was the change in U

All that matters are the initial and final equilibrium states of the gas inside the piston. To determine the final state you just need to know how much energy was extracted during the process and that just depends on the amount of work done.

The difficulty in real life would be in determining the work done because the gas in the piston would be applying a force not only to overcome opposing pressure and friction on the piston but also to accelerate the piston. That is why the problem is simplified by making the piston massless and frictionless and making the opposing pressure, P1, constant.

So, with the given facts, the work done by the gas inside the cylinder in this irreversible expansion is simply P1ΔV=P1(V1-V0). Applying the first law (Q=0 as it is adiabatic): ΔU=-W=-P1(V1-V0)=nC_VΔT

(c). What was the change in entropy for the reversible processes? What was the change in entropy of the irreversible process?

The change in entropy just depends on the initial and final states. Those states are determined by the process, of course. An adiabatic free expansion of an ideal gas does not result in a change in internal energy but a fast irreversible adiabatic change against a non-zero external pressure does some work so the internal energy will decrease. But the bottom line is all you need to know to determine the initial and final states is how much energy was transferred into or out of the system by means of heat flow or macroscopic work.

Once you have determined the initial and final states (by determining Q and W) the entropy change is:
$\Delta S=\int_{i}^{f} \frac{dQ_{rev}}{T}$
over a reversible path between the two states.

In the case of the expanding piston, you can determine the change in pressure from the change in temperature. So a reversible process between those two states would be comprised of a reversible isothermal expansion followed by a reversible isochoric cooling. The reversible heat flow in the isothermal part will be equal to the work done by the gas:
$Q_{rev1} = W = \int PdV = nRT_0\ln(\frac{V_1}{V_0})$.
The reversible heat flow in the isochoric cooling will be $Q_{rev2}=nC_V\Delta T$. So:

$\Delta S=\frac{Q_{rev1}}{T_0} + \int_{T_0}^{T_1} \frac{nC_vdT}{T}=nR\ln(\frac{V_1}{V_0}) + nC_v\ln({\frac{T_1}{T_0}})$

AM